
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,且橢圓上存在一點
,且橢圓上存在一點![]() ,滿足
,滿足![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過橢圓![]() 右焦點
右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于不同的兩點
交于不同的兩點![]() ,求
,求![]() 的內切圓的半徑的最大值.
的內切圓的半徑的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用余弦定理和橢圓的定義即可求出a,再根據b2=a2﹣c2=3,可得橢圓的方程;(2)設A(x1,y1),B(x2,y2),設△F1AB的內切圓的半徑為R,表示出△F1AB的周長與面積,設直線l的方程為x=my+1,聯立直線與橢圓方程,利用韋達定理,表示三角形面積,令t![]() ,利用函數的單調性求解面積的最大值,然后求解△F1AB內切圓半徑的最大值為
,利用函數的單調性求解面積的最大值,然后求解△F1AB內切圓半徑的最大值為![]() .
.
(1)設![]() ,則
,則![]() 內,
內,
由余弦定理得![]() ,化簡得
,化簡得![]() ,解得
,解得![]()
故![]() ,得
,得![]()
所以橢圓![]() 的標準方程為
的標準方程為![]()
(2)設![]() ,設
,設![]() 得內切圓半徑為
得內切圓半徑為![]()
![]() 的周長為
的周長為![]()
所以![]()
根據題意知,直線![]() 的斜率不為零,可設直線
的斜率不為零,可設直線![]() 的方程為
的方程為![]()
由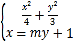 得
得![]()
![]()
由韋達定理得![]()
![]()
![]()
令![]() ,則
,則![]()
令![]() ,則
,則![]() 時,
時,![]() 單調遞增,
單調遞增,
![]()
即當![]() 時,
時,![]() 的最大值為
的最大值為![]() ,此時
,此時![]() .
.
故當直線![]() 的方程為
的方程為![]() 時,
時,![]() 內圓半徑的最大值為
內圓半徑的最大值為![]() .
.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】在梯形![]() 中,
中,![]() ,
,![]() 為
為![]() 的中點,線段
的中點,線段![]() 與
與![]() 交于
交于![]() 點(如圖1).將
點(如圖1).將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 為直二面角(如圖2).
為直二面角(如圖2).
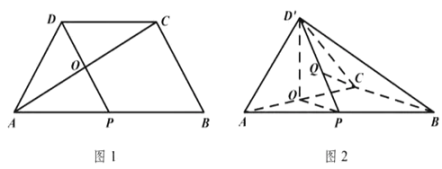
(1)求證:![]() 平面
平面![]() ;
;
(2)線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市收集并整理了該市2017年1月份至10月份每月份最低氣溫與最高氣溫(單位:![]() )的數據,繪制了折線圖(如圖).已知該市每月的最低氣溫與當月的最高氣溫兩變量具有較好的線性關系,則根據該折線圖,下列結論錯誤的是()
)的數據,繪制了折線圖(如圖).已知該市每月的最低氣溫與當月的最高氣溫兩變量具有較好的線性關系,則根據該折線圖,下列結論錯誤的是()
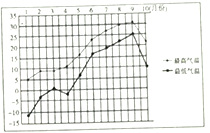
A. 最低氣溫低于![]() 的月份有
的月份有![]() 個
個
B. ![]() 月份的最高氣溫不低于
月份的最高氣溫不低于![]() 月份的最高氣溫
月份的最高氣溫
C. 月溫差(最高氣溫減最低氣溫)的最大值出現在![]() 月份
月份
D. 每月份最低氣溫與當月的最高氣溫兩變量為正相關
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是從0,1,2,3,4五個數中任取的一個數,
是從0,1,2,3,4五個數中任取的一個數,![]() 是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
是從0,1,2三個數中任取的一個數,求上述方程有實根的概率;
(2)若![]() 是從區間
是從區間![]() 上任取的一個數,
上任取的一個數,![]() 是從區間
是從區間![]() 上任取的一個數,求上述方程有實根的概率.
上任取的一個數,求上述方程有實根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新個稅法于2019年1月1日進行實施.為了調查國企員工對新個稅法的滿意程度,研究人員在![]() 地各個國企中隨機抽取了1000名員工進行調查,并將滿意程度以分數的形式統計成如下的頻率分布直方圖,其中
地各個國企中隨機抽取了1000名員工進行調查,并將滿意程度以分數的形式統計成如下的頻率分布直方圖,其中![]() .
.
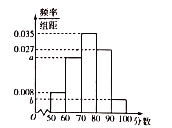
(1)求![]() 的值并估計被調查的員工的滿意程度的中位數;(計算結果保留兩位小數)
的值并估計被調查的員工的滿意程度的中位數;(計算結果保留兩位小數)
(2)若按照分層抽樣從![]() ,
,![]() 中隨機抽取8人,再從這8人中隨機抽取2人,求至少有1人的分數在
中隨機抽取8人,再從這8人中隨機抽取2人,求至少有1人的分數在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中,錯誤的是( )
A.圓錐所有的軸截面是全等的等腰三角形
B.圓柱的軸截面是過母線的截面中面積最大的一個
C.圓錐的軸截面是所有過頂點的界面中面積最大的一個
D.當球心到平面的距離小于球面半徑時,球面與平面的交線總是一個圓
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新個稅法于2019年1月1日進行實施.為了調查國企員工對新個稅法的滿意程度,研究人員在![]() 地各個國企中隨機抽取了1000名員工進行調查,并將滿意程度以分數的形式統計成如下的頻率分布直方圖,其中
地各個國企中隨機抽取了1000名員工進行調查,并將滿意程度以分數的形式統計成如下的頻率分布直方圖,其中![]() .
.
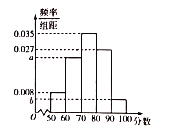
(1)求![]() 的值并估計被調查的員工的滿意程度的中位數;(計算結果保留兩位小數)
的值并估計被調查的員工的滿意程度的中位數;(計算結果保留兩位小數)
(2)若按照分層抽樣從![]() ,
,![]() 中隨機抽取8人,再從這8人中隨機抽取2人,求至少有1人的分數在
中隨機抽取8人,再從這8人中隨機抽取2人,求至少有1人的分數在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,橢圓短軸的一個端點與兩個焦點構成的三角形的面積為
,橢圓短軸的一個端點與兩個焦點構成的三角形的面積為![]() ,直線l的方程為:
,直線l的方程為:![]()
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知直線l與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點
兩點
①若線段![]() 中點的橫坐標為
中點的橫坐標為![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知點![]() ,求證:
,求證:![]() 為定值
為定值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com