【題目】已知函數
，
.
（Ⅰ）討論
的單調性；
（Ⅱ）
使得
成立，求實數
的取值范圍.
【答案】（Ⅰ）答案不唯一，具體見解析（Ⅱ）
或
【解析】
（Ⅰ）求出函數的導數，通過討論
的范圍，求出函數的單調區間即可。
（Ⅱ）由于
時，
，若要
使得
成立，只需
時，
成立，利用導數討論
的最大值和
的最小值，即可求出實數的取值范圍。
（Ⅰ）由題可得
的定義域為
，
，
當
時，
，解得
，或
，
，解得
，
∴在
，
上是增函數，在
上是減函數；
當
時，，解得
，或
，，解得
，
∴在
，
上是增函數，在
上是減函數；
當
時，
恒成立，且只在
時
，∴在上是增函數.
（Ⅱ）時，，
若要使得成立，
只需時，成立，
由（Ⅰ）知當
時，在
上是增函數，
，
當
時，在
上是減函數，在
上是增函數，
，
當時，在上是減函數，
，
，對稱軸
，
當時，
在上是增函數，
，
，解得
，∴，
當時，在
上是增函數，在
上是減函數，
，
，
整理得
，∵，∴只需
，
令
，
，當
時，
，
在
上是增函數，又
，∴時，
，∴
.
當時，在上是減函數，
，
，解得，
綜上所述，或.
科目：高中數學 來源： 題型：
【題目】如圖，點M，N分別為正方體ABCD﹣A1B1C1D1的棱AA1，BB1的中點，以正方體的六個面的中心為頂點構成一個八面體，若平面D1MNC1將該八面體分割成上、下兩部分的體積分別為V1、V2，則
（ ）
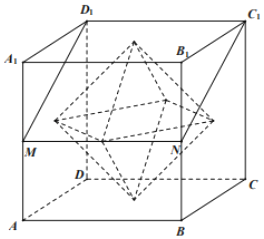
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,五邊形
中,四邊形
為長方形,
為邊長為
的正三角形,將沿
折起,使得點
在平面上的射影恰好在
上.
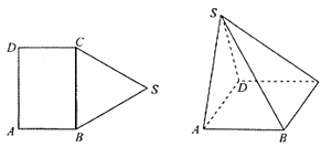
（Ⅰ）當
時,證明:平面
平面
；
（Ⅱ）若
,求平面與平面
所成二面角的余弦值的絕對值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線的頂點在原點，焦點
在
軸的正半軸，且過點
，過的直線交拋物線于
，
兩點.
（1）求拋物線的方程；
（2）設直線
是拋物線的準線，求證：以
為直徑的圓與直線相切.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】撫州市某中學利用周末組織教職員工進行了一次秋季登軍峰山健身的活動，有
人參加，現將所有參加人員按年齡情況分為
，
，
，
，
，
，
等七組，其頻率分布直方圖如下圖所示．已知之間的參加者有4人．
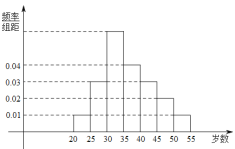
（1）求和之間的參加者人數
；
（2）組織者從
之間的參加者（其中共有
名女教師包括甲女，其余全為男教師）中隨機選取
名擔任后勤保障工作，求在甲女必須入選的條件下，選出的女教師的人數為2人的概率.
（3）已知和之間各有
名數學教師，現從這兩個組中各選取人擔任接待工作，設兩組的選擇互不影響，求兩組選出的人中都至少有
名數學教師的概率?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
