
【題目】天干地支紀年法,源于中國,中國自古便有十天干與十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支紀年法是按順序以一個天干和一個地支相配,排列起來,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年為“甲子”,第二年為“乙丑”,第三年為“丙寅”,…,以此類推,排列到“癸酉”后,天干回到“甲”重新開始,即“甲戌”,“乙亥”,之后地支回到“子”重新開始,即“丙子”,…,以此類推,已知2016年為丙申年,那么到改革開放100年時,即2078年為________年
科目:高中數學 來源: 題型:
【題目】下列說法:
①將一組數據中的每個數據都加上或減去同一個常數后,方差恒不變;
②設有一個回歸方程![]() ,變量x增加一個單位時,y平均增加5個單位;
,變量x增加一個單位時,y平均增加5個單位;
③線性回歸方程![]() 必過
必過![]() ;
;
④在一個![]() 列聯表中,由計算得是
列聯表中,由計算得是![]() ,則有
,則有![]() 的把握確認這兩個變量間有關系.
的把握確認這兩個變量間有關系.
其中錯誤的個數是( )
本題可以參考獨立性檢驗臨界值表:
| 0.05 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知奇函數f(x)![]() ,函數g(θ)=cos2θ+2sinθ
,函數g(θ)=cos2θ+2sinθ![]() ,θ∈[m,
,θ∈[m,![]() ].m,b∈R.
].m,b∈R.
(1)求b的值;
(2)判斷函數f(x)在[0,1]上的單調性,并證明;
(3)當x∈[0,1]時,函數g(θ)的最小值恰為f(x)的最大值,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,橢圓
中,橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸上,且過點
軸上,且過點![]() ,若
,若![]() 的兩焦點與其中一個頂點能構成一個等邊三角形.
的兩焦點與其中一個頂點能構成一個等邊三角形.
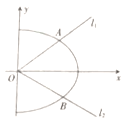
(1)求![]() 的方程.
的方程.
(2)已知過![]() 的兩條直線
的兩條直線![]() ,
,![]() (斜率都存在)與
(斜率都存在)與![]() 的右半部分(
的右半部分(![]() 軸右側)分別相交于
軸右側)分別相交于![]() ,
,![]() 兩點,且
兩點,且![]() 的面積為
的面積為![]() ,試判斷
,試判斷![]() ,
,![]() 的斜率之積是否為定值?若是,求出定值;若不是,說明理由.
的斜率之積是否為定值?若是,求出定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高速公路服務區臨時停車場按時段收費,收費標準:每輛汽車一次停車不超過1小時收費5元,超過1小時的部分每小時收費7元(不足1小時的部分按1小時計算).現有甲、乙兩人在該服務區臨時停車,兩人停車都不超過4小時.
(1)若甲停車1小時以上且不超過2小時的概率為![]() ,停車付費多于12元的概率為
,停車付費多于12元的概率為![]() ,求甲停車付費恰為5元的概率;
,求甲停車付費恰為5元的概率;
(2)若每人停車的時長在每個時段的可能性相同,求甲、乙兩人停車付費之和為38元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若對任意的正整數![]() ,總存在正整數
,總存在正整數![]() ,使得數列
,使得數列![]() 的前
的前![]() 項和
項和![]() ,則稱數列
,則稱數列![]() 是“回歸數列”.
是“回歸數列”.
(1)前![]() 項和為
項和為![]() 的數列
的數列![]() 是否是“回歸數列”?并請說明理由;
是否是“回歸數列”?并請說明理由;
(2)設![]() 是等差數列,首項
是等差數列,首項![]() ,公差
,公差![]() ,若
,若![]() 是“回歸數列”,求
是“回歸數列”,求![]() 的值;
的值;
(3)是否對任意的等差數列![]() ,總存在兩個“回歸數列”
,總存在兩個“回歸數列”![]() 和
和![]() ,使得
,使得![]() (
(![]() )成立,請給出你的結論,并說明理由.
)成立,請給出你的結論,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】階梯水價的原則是“保基本、建機制、促節約”,其中“保基本”是指保證至少80%的居民用戶用水價格不變.為響應國家政策,制訂合理的階梯用水價格,某城市采用簡單隨機抽樣的方法分別從郊區和城區抽取5戶和20戶居民的年人均用水量進行調研,得到數據如下(單位:噸).
郊區:19 25 28 32 34
城區:18 19 21 22 22 23 23 23 24 25 26 27 28 28 28 29 29 31 35 42
(1)在郊區的這5戶居民中隨機抽取2戶,求其年人均用水量都不超過30噸的概率;
(2)設該城市郊區和城區的居民戶數比為1:5,現將年人均用水量不超過30噸的用戶定義為第一階梯用戶,并保證這一階梯的居民用戶用水價格保持不變,試根據樣本總體的思想,分析此方案是否符合國家“保基本”政策.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】12個朋友每周聚餐一次,每周他們分成三組,每組4人,不同組坐不同的桌子.若要求這些朋友中任意兩個人至少有一次同坐一張桌子,則至少需要周____周.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com