
【題目】如圖,三棱柱![]() 中,四邊形
中,四邊形![]() 為菱形,
為菱形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 在線段
在線段![]() 上移動(dòng),
上移動(dòng),![]() 為棱
為棱![]() 的中點(diǎn).
的中點(diǎn).
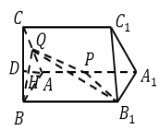
(1)若![]() 為線段
為線段![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 中點(diǎn),延長
中點(diǎn),延長![]() 交
交![]() 于
于![]() ,求證:
,求證:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角的余弦值為
的平面角的余弦值為![]() ,求點(diǎn)
,求點(diǎn)![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)見解析(2)![]()
【解析】
(1)取BB1中點(diǎn)E,連接AE,EH,推導(dǎo)出EH∥B1Q,AE∥PB1,從而平面EHA∥平面B1QP,由此能證明AD∥平面B1PQ.
(2)連接PC1,AC1,推導(dǎo)出AA1=AC=A1C1=4,△AC1A1為正三角形,推導(dǎo)出PC1⊥AA1,從而PC1⊥平面ABB1A1,建立空間直角坐標(biāo)系Pxyz,利用向量法能求出點(diǎn)P到平面BQB1的距離.
解:(1)證明:如圖,取![]() 中點(diǎn)
中點(diǎn)![]() ,連接
,連接![]()
∵![]() 為
為![]() 中點(diǎn),∴
中點(diǎn),∴![]()
在平行四邊形![]() 中,
中,![]() 分別為
分別為![]() 的中點(diǎn),∴
的中點(diǎn),∴![]()
又![]() ,
,![]() ,
,
∴平面![]() 平面
平面![]()
∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.

(2)連接![]() ,
,
∵四邊形![]() 為菱形,∴
為菱形,∴![]()
又![]() ,∴
,∴![]() 為正三角形
為正三角形
∵![]() 為
為![]() 的中點(diǎn),∴
的中點(diǎn),∴![]()
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
在平面![]() 內(nèi)過點(diǎn)
內(nèi)過點(diǎn)![]() 作
作![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]()
建立如圖所示的空間直角坐標(biāo)系![]() ,則
,則

![]() ,
,
設(shè)![]() ,
,
∴![]() ,
,
∴![]()
![]()
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]()
![]()
設(shè)平面![]() 的法向量為
的法向量為![]() ,
,
則 得
得![]() ,令
,令![]() ,則
,則![]() ,
,
∴平面![]() 的一個(gè)法向量為
的一個(gè)法向量為![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]() ,二面角
,二面角![]() 的平面角為
的平面角為![]() ,
,
則
∴![]() 或
或![]() (舍),∴
(舍),∴![]() ,∴
,∴![]() .
.
又![]() ,∴
,∴![]() ,∴
,∴![]()
連接![]() ,設(shè)點(diǎn)
,設(shè)點(diǎn)![]() 到平面
到平面![]() 的距離為
的距離為![]() ,則
,則![]()
∴![]() ,即點(diǎn)
,即點(diǎn)![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數(shù)多少之間的關(guān)系,他們分別到氣象局與某醫(yī)院抄錄了1至6月份每月10號(hào)的晝夜溫差情況與因患感冒而就診的人數(shù),得到如表資料:
日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就診人數(shù)y(個(gè)) | 22 | 25 | 29 | 26 | 16 | 12 |
該興趣小組確定的研究方案是:先從這六組數(shù)據(jù)中選取2組,用剩下的4組數(shù)據(jù)求線性回歸方程,再用被選取的2組數(shù)據(jù)進(jìn)行檢驗(yàn).
(1)求選取的2組數(shù)據(jù)恰好是相鄰兩個(gè)月的概率;
(2)若選取的是1月與6月的兩組數(shù)據(jù),請(qǐng)根據(jù)2至5月份的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計(jì)數(shù)據(jù)與所選出的檢驗(yàn)數(shù)據(jù)的誤差均不超過2人,則認(rèn)為得到的線性回歸方程是理想的,試問(2)中所得線性回歸方程是否理想?
參考公式: ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() (
(![]() 為自然對(duì)數(shù)的底數(shù)),
為自然對(duì)數(shù)的底數(shù)),![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的極小值;
的極小值;
(2)當(dāng)![]() 時(shí),關(guān)于
時(shí),關(guān)于![]() 的方程
的方程![]() 有且只有一個(gè)實(shí)數(shù)解,求實(shí)數(shù)
有且只有一個(gè)實(shí)數(shù)解,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 經(jīng)過兩點(diǎn)
經(jīng)過兩點(diǎn)![]() ,
,![]() ,且圓心
,且圓心![]() 在直線
在直線![]() :
:![]() 上.
上.
(1)求圓![]() 的方程;
的方程;
(2)設(shè)圓![]() 與
與![]() 軸相交于
軸相交于![]() 、
、![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 為圓
為圓![]() 上不同于
上不同于![]() 、
、![]() 的任意一點(diǎn),直線
的任意一點(diǎn),直線![]() 、
、![]() 交
交![]() 軸于
軸于![]() 、
、![]() 點(diǎn).當(dāng)點(diǎn)
點(diǎn).當(dāng)點(diǎn)![]() 變化時(shí),以
變化時(shí),以![]() 為直徑的圓
為直徑的圓![]() 是否經(jīng)過圓
是否經(jīng)過圓![]() 內(nèi)一定點(diǎn)?請(qǐng)證明你的結(jié)論.
內(nèi)一定點(diǎn)?請(qǐng)證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的有( )
(1)很小的實(shí)數(shù)可以構(gòu)成集合;
(2)集合![]() 與集合
與集合![]() 是同一個(gè)集合;
是同一個(gè)集合;
(3) ![]() 這些數(shù)組成的集合有5個(gè)元素;
這些數(shù)組成的集合有5個(gè)元素;
(4)任何集合至少有兩個(gè)子集.
A.0個(gè)B.1個(gè)C.2個(gè)D.3個(gè)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 和
和![]() 都是定義在集合
都是定義在集合![]() 上的函數(shù),對(duì)于任意的
上的函數(shù),對(duì)于任意的![]() ,都有
,都有![]() 成立,稱函數(shù)
成立,稱函數(shù)![]() 與
與![]() 在
在![]() 上互為“互換函數(shù)”.
上互為“互換函數(shù)”.
(1)函數(shù)![]() 與
與![]() 在
在![]() 上互為“互換函數(shù)”,求集合
上互為“互換函數(shù)”,求集合![]() ;
;
(2)若函數(shù)![]() (
(![]() 且
且![]() )與
)與![]() 在集合
在集合![]() 上互為“互換函數(shù)”,求證:
上互為“互換函數(shù)”,求證:![]() ;
;
(3)函數(shù)![]() 與
與![]() 在集合
在集合![]() 且
且![]() 上互為“互換函數(shù)”,當(dāng)
上互為“互換函數(shù)”,當(dāng)![]() 時(shí),
時(shí),![]() ,且
,且![]() 在
在![]() 上是偶函數(shù),求函數(shù)
上是偶函數(shù),求函數(shù)![]() 在集合
在集合![]() 上的解析式.
上的解析式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】等差數(shù)列的定義可用數(shù)學(xué)符號(hào)語言描述為________,其中![]() ,其通項(xiàng)公式
,其通項(xiàng)公式![]() _________,
_________,![]() __________=_________,等差數(shù)列中,若
__________=_________,等差數(shù)列中,若![]() 則________(
則________(![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在某屆世界杯足球賽上,a,b,c,d四支球隊(duì)進(jìn)入了最后的比賽,在第一輪的兩場比賽中,a對(duì)b,c對(duì)d,然后這兩場比賽的勝者將進(jìn)入冠亞軍決賽,這兩場比賽的負(fù)者比賽,決出第三名和第四名.比賽的一種最終可能結(jié)果記為acbd(表示a勝b,c勝d,然后a勝c,b勝d).
(1)寫出比賽所有可能結(jié)果構(gòu)成的樣本空間;
(2)設(shè)事件A表示a隊(duì)獲得冠軍,寫出A包含的所有可能結(jié)果;
(3)設(shè)事件B表示a隊(duì)進(jìn)入冠亞軍決賽,寫出B包含的所有可能結(jié)果.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】假設(shè)有5個(gè)條件類似的女孩(把她們分別記為A,B,C,D, E)應(yīng)聘秘書工作,但只有2個(gè)秘書職位,因此5個(gè)人中只有2人能被錄用.如果5個(gè)人被錄用的機(jī)會(huì)相等,分別計(jì)算下列事件的概率;
(1)女孩A得到一個(gè)職位;
(2)女孩A和B各得到一個(gè)職位;
(3)女孩A或B得到一個(gè)職位.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com