
【題目】若點( ![]() ,2)在冪函數f(x)的圖象上,點(2,
,2)在冪函數f(x)的圖象上,點(2, ![]() )在冪函數g(x)的圖象上,定義h(x)=
)在冪函數g(x)的圖象上,定義h(x)= ![]() 求函數h(x)的最大值及單調區間.
求函數h(x)的最大值及單調區間.
【答案】解:設f(x)=xn , g(x)=xm , 由題意可得2=( ![]() )n , 解得n=2,
)n , 解得n=2,
即有f(x)=x2;![]() =2m , 解得m=﹣1,即有g(x)=x﹣1 .
=2m , 解得m=﹣1,即有g(x)=x﹣1 .
由f(x)=g(x),可得x=1,
即有h(x)=  ;
;
當0<x≤1時,h(x)遞增,可得0<h(x)≤1;
當x>1或x<0時,h(x)遞減,可得h(x)∈(0,1)∪(﹣∞,0),
即有h(x)的最大值為1;
增區間為(0,1];減區間為(﹣∞,0),(1,+∞)
【解析】設f(x)=xn , g(x)=xm , 代入點的坐標,解方程可得f(x),g(x)的解析式,再由定義,求得h(x)的解析式,通過二次函數和反比例函數的性質,可得最大值和單調區間.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分別是PC,PD,BC的中點. 
(1)求證:平面PAB∥平面EFG;
(2)在線段PB上確定一點Q,使PC⊥平面ADQ,并給出證明;
(3)求出D到平面EFG的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一個關于平面圖形的命題:如圖,同一個平面內有兩個邊長都是a的正方形,其中一個的某頂點在另一個的中心,則這兩個正方形重疊部分的面積恒為 ![]() .類比到空間,有兩個棱長均為a的正方體,其中一個的某頂點在另一個的中心,則這兩個正方體重疊部分的體積恒為 .
.類比到空間,有兩個棱長均為a的正方體,其中一個的某頂點在另一個的中心,則這兩個正方體重疊部分的體積恒為 . 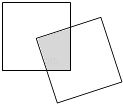
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)
某學校簡單隨機抽樣方法抽取了100名同學,對其日均課外閱讀時間:(單位:分鐘)進行調查,結果如下:

若將日均課外閱讀時間不低于60分鐘的學生稱為“讀書迷”
(1)將頻率視為概率,估計該校4000名學生中“讀書迷”有多少人?
(2)從已抽取的8名“讀書迷”中隨機抽取4位同學參加讀書日宣傳活動.
①求抽取的4為同學中有男同學又有女同學的概率;
②記抽取的“讀書迷”中男生人數為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=2+log3x,x∈[1,9],g(x)=[f(x)]2+f(x2),
(1)求g(x)的定義域;
(2)求g(x)的最大值以及g(x)取最大值時x的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了100個網箱,測量各箱水產品的產量(單位:kg)其頻率分布直方圖如下:
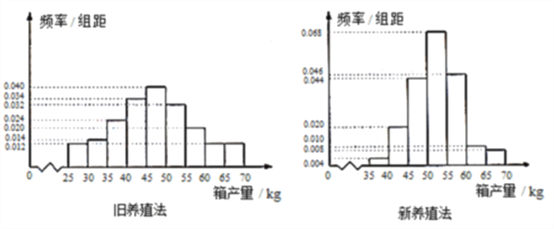
(1) 記![]() 表示事件“舊養殖法的箱產量低于50kg”,估計
表示事件“舊養殖法的箱產量低于50kg”,估計![]() 的概率;
的概率;
(2)填寫下面聯表,并根據列聯表判斷是否有![]() %的把握認為箱產量與養殖方法有關:
%的把握認為箱產量與養殖方法有關:
箱產量 | 箱產量 | |
舊養殖法 | ||
新養殖法 |
(3)根據箱產量的頻率分布直方圖,對兩種養殖方法的優劣進行比較.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
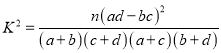
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數f(x)= ![]() 是奇函數.
是奇函數.
(Ⅰ)求a,b的值;
(Ⅱ)若對任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=( ![]() )x , g(x)=x2 , 對于不相等的實數x1 , x2 , 設m=
)x , g(x)=x2 , 對于不相等的實數x1 , x2 , 設m= ![]() ,n=
,n= ![]() ,則下列說法正確的有( )
,則下列說法正確的有( )
①對于任意不相等的實數x1 , x2 , 都有m<0;
②對于任意不相等的實數x1 , x2 , 都有n<0;
③存在不相等的實數x1 , x2 , 使得m=n.
A.①
B.①③
C.②③
D.①②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com