
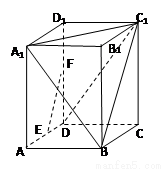
(本題滿分10分) 在長方體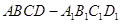 中,
中,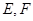 分別是
分別是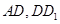 的中點,
的中點,
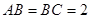 ,
,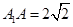 .
.
(Ⅰ)求證: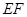 //平面
//平面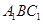 ;
;
(Ⅱ)在線段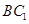 上是否存在點
上是否存在點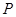 ,使直線
,使直線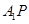 與
與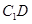 垂直,
垂直,
如果存在,求線段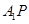 的長,如果不存在,請說明理由.
的長,如果不存在,請說明理由.
(Ⅰ)見解析;(Ⅱ)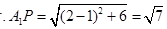 .
.
【解析】
試題分析:(1)根據(jù)已知中的長方體的性質(zhì),結(jié)合線線平行,得到線面平行的證明。
(2)由于根據(jù)已知條件可知線A1D1垂直于平面CD1,進而利用性質(zhì)定理得到線線垂直,相似來求解長度。
解:(Ⅰ)連接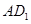 ,在長方體
,在長方體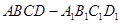 中,
中,
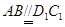 ,則四邊形
,則四邊形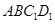 是平行四邊形,∴
是平行四邊形,∴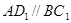 ,又∵
,又∵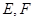 分別是
分別是 的中點∴
的中點∴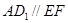 ,∴
,∴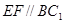 ,又
,又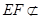 面
面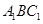 ,
,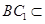 面
面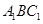 ,
,
∴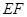 //平面
//平面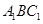 (3分)
(3分)
(Ⅱ)在平面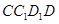 中作
中作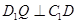 交
交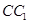 于
于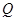 ,過
,過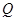 作
作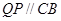 交
交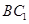 于點
于點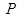 ,連
,連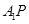 ∵
∵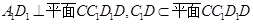
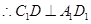
而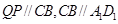
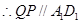 又
又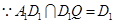
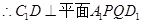 ∵
∵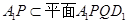
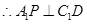
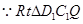 ∽
∽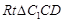
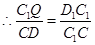
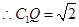
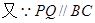
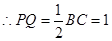
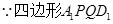 為直角梯形,且高
為直角梯形,且高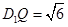
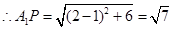 .(10分)
.(10分)
考點:本題主要是考查線面平行的判定以及線線垂直的證明運用。
點評:解決該試題的關(guān)鍵是熟練的利用線面平行的判定定理,得到線線平行進而得到證明,同時線面的垂直,結(jié)合相似得到求解。


 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數(shù)學 來源: 題型:
(本題滿分10分) 已知:![]() (
(![]() R,a為常數(shù)).
R,a為常數(shù)).
(I)若![]() ,求f(x)的最小正周期及單調(diào)減區(qū)間;
,求f(x)的最小正周期及單調(diào)減區(qū)間;
(II)若![]() ,
,![]() 時,f(x)的最大值為4,求a的值.
時,f(x)的最大值為4,求a的值.
查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年上海市黃浦區(qū)高三上學期期終基礎(chǔ)學業(yè)測評理科數(shù)學試卷 題型:解答題
(本題滿分16分)本題共有2個小題,第1小題滿分6分,第2小題滿分10分.
已知兩點 、
、 ,點
,點 是直角坐標平面上的動點,若將點
是直角坐標平面上的動點,若將點 的橫坐標保持不變、縱坐標擴大到
的橫坐標保持不變、縱坐標擴大到 倍后得到點
倍后得到點 滿足
滿足 .
.
(1) 求動點 所在曲線
所在曲線 的軌跡方程;
的軌跡方程;
(2)(理科)過點 作斜率為
作斜率為 的直線
的直線 交曲線
交曲線 于
于 兩點,且滿足
兩點,且滿足 ,又點
,又點 關(guān)于原點O的對稱點為點
關(guān)于原點O的對稱點為點 ,試問四點
,試問四點 是否共圓,若共圓,求出圓心坐標和半徑;若不共圓,請說明理由.
是否共圓,若共圓,求出圓心坐標和半徑;若不共圓,請說明理由.
(文科)過點 作斜率為
作斜率為 的直線
的直線 交曲線
交曲線 于
于 兩點,且滿足
兩點,且滿足 (O為坐標原點),試判斷點
(O為坐標原點),試判斷點 是否在曲線
是否在曲線 上,并說明理由.
上,并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
選修4—4 參數(shù)方程與極坐標(本題滿分10分)
已知圓![]() 和圓
和圓![]() 的極坐標方程分別為
的極坐標方程分別為![]() ,
,![]() .
.
(1)把圓![]() 和圓
和圓![]() 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(2)求經(jīng)過兩圓交點的直線的極坐標方程.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com