
(16分)已知:數列![]() ,
,![]() 中,
中,![]() =0,
=0,![]() =1,且當
=1,且當![]() 時,
時,![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,![]() ,
,![]() ,
,![]() 成等比數列.
成等比數列.
(1)求數列![]() ,
,![]() 的通項公式;
的通項公式;
(2)求最小自然數![]() ,使得當
,使得當![]() ≥
≥![]() 時,對任意實數
時,對任意實數![]()
![]() ,不等式
,不等式![]()
![]() ≥
≥![]()
![]()
![]() 恒成立;
恒成立;![]()
(3)設![]() (
(![]() ∈
∈![]() ),求證:當
),求證:當![]() ≥2都有
≥2都有![]() >2
>2![]() .
.
解析:(1) ∵當![]() ∈
∈![]() 時,
時,![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,![]() ,
,![]() ,
,![]() 成等比數列.
成等比數列.
∴2![]() =
=![]() +
+![]() ,
, ![]() =
=![]() . ………………………………………2分
. ………………………………………2分
又∵![]() ,
,![]() ,∴
,∴![]() ≥0,
≥0,![]() ≥0 , 且
≥0 , 且![]() ,
,
∴![]() (
(![]() ≥2),………………………………………………4分
≥2),………………………………………………4分
∴數列![]() 是等差數列,又
是等差數列,又![]() ,∴
,∴![]() ,
,![]() 也適合.
也適合.
∴![]() ,
, ![]() . ………………………………………………………6分
. ………………………………………………………6分
(2) 將![]() ,
,![]() 代入不等式
代入不等式![]()
![]() ≥
≥![]()
![]()
![]() (
(![]() )
)
整理得:![]() ≥0 ………………………………………………8分
≥0 ………………………………………………8分
令![]()
![]() ,則
,則![]() 是關于
是關于![]() 的一次函數,
的一次函數,
由題意可得![]() ∴
∴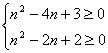 ,解得
,解得![]() ≤1或
≤1或![]() ≥3.
≥3.
∴存在最小自然數![]() ,使得當
,使得當![]() ≥
≥![]() 時,不等式(
時,不等式(![]() )恒成立.…………………10分
)恒成立.…………………10分
(3) 由(1)得:![]() …+
…+![]() .∴
.∴![]() ,
,![]() (
(![]() ≥2),
≥2),
∴ ![]() …………………………………………………12分
…………………………………………………12分
由(![]() )+(
)+(![]() )+…+(
)+…+(![]() )
)
![]() …+
…+![]() )
)![]() …+
…+![]() ,
,
即:![]()
![]() …+
…+![]() )
)![]() …+
…+![]() ……………………14分
……………………14分
∵![]() …+
…+![]() <
<![]() …+
…+![]()
=![]() …+
…+![]()
=![]() <1
<1


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:高中數學 來源:2010年廣東省梅州市曾憲梓中學高二上學期10月月考數學卷 題型:解答題
(本小題滿分16分)已知數列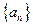 :
: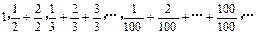
①觀察規律,歸納并計算數列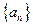 的通項公式,它是個什么數列?
的通項公式,它是個什么數列?
②若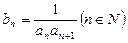 ,設
,設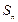 =
= ,求
,求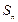 。
。
③設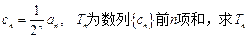
查看答案和解析>>
科目:高中數學 來源:2011屆江蘇省泰州市高三第一次模擬考試數學卷 題型:解答題
(本小題滿分16分)已知在直角坐標系中, ,其中數列
,其中數列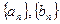 都是遞增數列。
都是遞增數列。
(1)若 ,判斷直線
,判斷直線 與
與 是否平行;
是否平行;
(2)若數列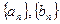 都是正項等差數列,設四邊形
都是正項等差數列,設四邊形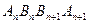 的面積為
的面積為 .
.
求證: 也是等差數列;
也是等差數列;
(3)若 ,
, ,記直線
,記直線 的斜率為
的斜率為 ,數列
,數列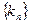 前8項依次遞減,求滿足條件的數列
前8項依次遞減,求滿足條件的數列 的個數。
的個數。
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省無錫市高三上學期期中考試數學(解析版) 題型:解答題
.(本題滿分16分)
已知等差數列 的首項為
的首項為 ,公差為b,等比數列
,公差為b,等比數列 的首項為b,公比為a(其中a,b均為正整數)。
的首項為b,公比為a(其中a,b均為正整數)。
(I)若 ,求數列
,求數列 的通項公式;
的通項公式;
(II)對于(1)中的數列 ,對任意
,對任意 在
在 之間插入
之間插入 個2,得到一個新的數列
個2,得到一個新的數列 ,試求滿足等式
,試求滿足等式 的所有正整數m的值;
的所有正整數m的值;
(III)已知 ,若存在正整數m,n以及至少三個不同的b值使得等
,若存在正整數m,n以及至少三個不同的b值使得等 成立,求t的最小值,并求t最小時a,b的值。
成立,求t的最小值,并求t最小時a,b的值。
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省泰州市高三第一次模擬考試數學卷 題型:解答題
(本小題滿分16分)已知在直角坐標系中, ,其中數列
,其中數列 都是遞增數列。
都是遞增數列。
(1)若 ,判斷直線
,判斷直線 與
與 是否平行;
是否平行;
(2)若數列 都是正項等差數列,設四邊形
都是正項等差數列,設四邊形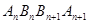 的面積為
的面積為 .
.
求證: 也是等差數列;
也是等差數列;
(3)若 ,
, ,記直線
,記直線 的斜率為
的斜率為 ,數列
,數列 前8項依次遞減,求滿足條件的數列
前8項依次遞減,求滿足條件的數列 的個數。
的個數。
查看答案和解析>>
科目:高中數學 來源:2010年廣東省梅州市高二上學期10月月考數學卷 題型:解答題
(本小題滿分16分)已知關于x的二次方程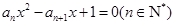 的兩根
的兩根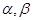 滿足
滿足 ,且
,且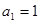
(1)試用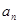 表示
表示 ;(2)求證:數列
;(2)求證:數列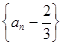 是等比數列;
是等比數列;
(3)求數列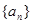 的前n項和
的前n項和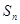 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com