
【題目】已知不等式![]() 對一切
對一切![]() 都成立,則
都成立,則![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】令![]() ,則
,則![]()
若a≤0,則y′>0恒成立,x>﹣1時函數遞增,無最值.
若a>0,由y′=0得:x=![]() ,
,
當﹣1<x<![]() 時,y′>0,函數遞增;
時,y′>0,函數遞增;
當x>![]() 時,y′<0,函數遞減.
時,y′<0,函數遞減.
則x=![]() 處取得極大值,也為最大值﹣lna+a﹣b﹣2,
處取得極大值,也為最大值﹣lna+a﹣b﹣2,
∴﹣lna+a﹣b﹣2≤0,
∴b≥﹣lna+a﹣2,
∴![]() ≥1﹣
≥1﹣![]() ﹣
﹣![]() ,
,
令t=1﹣![]() ﹣
﹣![]() ,
,
∴t′=![]() ,
,
∴(0,e﹣1)上,t′<0,(e﹣1,+∞)上,t′>0,
∴a=e﹣1,tmin=1﹣e.
∴![]() 的最小值為1﹣e.
的最小值為1﹣e.
點晴:本題主要考查用導數研究不等式恒成立問題. 解決這類問題的一種方法法是:通過變量分離將含參函數的問題轉化為不含參的確定函數的最值問題,本題中a≤0時,則y′>0恒成立,x>﹣1時函數遞增,無最值.a>0時x=![]() 處取得極大值,也為最大值﹣lna+a﹣b﹣2≤0,可得b≥﹣lna+a﹣2,于是
處取得極大值,也為最大值﹣lna+a﹣b﹣2≤0,可得b≥﹣lna+a﹣2,于是![]() ≥1﹣
≥1﹣![]() ﹣
﹣![]() ,令t=1﹣
,令t=1﹣![]() ﹣
﹣![]() ,然后利用導數研究這個函數的單調性、極值和最值,可得
,然后利用導數研究這個函數的單調性、極值和最值,可得![]() 的最小值.
的最小值.


 目標測試系列答案
目標測試系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() 的定義域為集合A,函數g(x)=lg(﹣x2+2x+m)的定義域為集合B.
的定義域為集合A,函數g(x)=lg(﹣x2+2x+m)的定義域為集合B.
(1)當m=3時,求A∩(RB)
(2)若A∩B={x|﹣1<x<4},求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
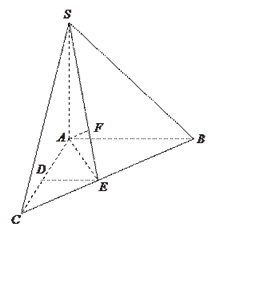
【題目】如圖,在三棱錐![]() 中,
中, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別是
分別是![]() ,
, ![]() 的中點,
的中點, ![]() 在
在![]() 上,且
上,且![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)在線段上![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角
![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() cosx(sinx+cosx).
cosx(sinx+cosx).
(1)若0<α< ![]() ,且sinα=
,且sinα= ![]() ,求f(α)的值;
,求f(α)的值;
(2)求函數f(x)的最小正周期及單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在[﹣1,1]上的奇函數,且f(1)=1,若x,y∈[﹣1,1],x+y≠0有(x+y)[f(x)+f(y)]>0.
(1)判斷f(x)的單調性,并加以證明;
(2)解不等式 ![]() ;
;
(3)若f(x)≤m2﹣2am+1對所有x∈[﹣1,1],a∈[﹣1,1]恒成立.求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某食品廠為了檢查甲、乙兩條自動包裝流水線的生產情況,隨機在這兩條流水線上各抽取40件產品作為樣本,并稱出它們的重量(單位:克),重量值落在![]() 內的產品為合格品,否則為不合格品,統計結果如表:
內的產品為合格品,否則為不合格品,統計結果如表:
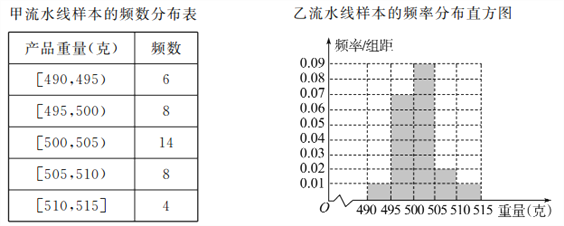
(Ⅰ)求甲流水線樣本合格的頻率;
(Ⅱ)從乙流水線上重量值落在![]() 內的產品中任取2個產品,求這2件產品中恰好只有一件合格的概率.
內的產品中任取2個產品,求這2件產品中恰好只有一件合格的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 在直角坐標系
在直角坐標系![]() 中的參數方程為
中的參數方程為![]() 為參數,
為參數, ![]() 為傾斜角),以坐標原點
為傾斜角),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,在極坐標系中,曲線的方程為
軸正半軸為極軸,建立極坐標系,在極坐標系中,曲線的方程為![]() .
.
(1)寫出曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)點![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求使
兩點,求使![]() 為定值的
為定值的![]() 值.
值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com