
【題目】已知函數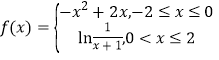 ,若
,若![]() 的圖象與
的圖象與![]() 軸有
軸有![]() 個不同的交點,則實數
個不同的交點,則實數![]() 的取值范圍是__________.
的取值范圍是__________.
【答案】![]()
【解析】試題分析:化簡 ,從而化g(x)=|f(x)|﹣ax﹣a的圖象與x軸有3個不同的交點為函數|f(x)|與函數y=ax+a的圖象有3個不同的交點;作函數的圖象,由數形結合求實數a的取值范圍.
,從而化g(x)=|f(x)|﹣ax﹣a的圖象與x軸有3個不同的交點為函數|f(x)|與函數y=ax+a的圖象有3個不同的交點;作函數的圖象,由數形結合求實數a的取值范圍.
詳解:
∵ ,
,
∴|f(x)|=![]() ,
,
∵g(x)=|f(x)|﹣ax﹣a的圖象與x軸有3個不同的交點,
∴函數|f(x)|與函數y=ax+a的圖象有3個不同的交點;
作函數|f(x)|與函數y=ax+a的圖象如下,
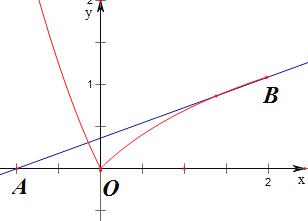
圖中A(﹣1,0),B(2,ln3),
故此時直線AB的斜率k=![]() ;
;
當直線AB與f(x)=ln(x+1)相切時,設切點為(x,ln(x+1));
則![]() =
=![]() ,
,
解得,x=e﹣1;
此時直線AB的斜率k=![]() ;
;
結合圖象可知,
![]() ≤a<
≤a<![]() ;
;
故答案為:![]() ≤a<
≤a<![]() .
.


 高效智能課時作業系列答案
高效智能課時作業系列答案科目:高中數學 來源: 題型:
【題目】在一次考試中某班級50名學生的成績統計如表,規定75分以下為一般,大于等于75分小于85分為良好,85分及以上為優秀.
![]()
經計算樣本的平均值![]() ,標準差
,標準差![]() . 為評判該份試卷質量的好壞,從其中任取一人,記其成績為
. 為評判該份試卷質量的好壞,從其中任取一人,記其成績為![]() ,并根據以下不等式進行評判
,并根據以下不等式進行評判
① ![]() ;
;
② ![]() ;
;
③ ![]()
評判規則:若同時滿足上述三個不等式,則被評為優秀試卷;若僅滿足其中兩個不等式,則被評為合格試卷;其他情況,則被評為不合格試卷.
(1)試判斷該份試卷被評為哪種等級;
(2)按分層抽樣的方式從3個層次的學生中抽出10名學生,再從抽出的10名學生中隨機抽出4人進行學習方法交流,用隨機變量![]() 表示4人中成績優秀的人數,求隨機變量
表示4人中成績優秀的人數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某蔬菜基地種植西紅柿,由歷年市場行情得知,從二月一日起的300天內,西紅柿市場銷售價與上市時間的關系用圖(1)的一條折線表示;西紅柿的種植成本與上市時間的關系用圖(2)的拋物線段表示.


(1)寫出圖(1)表示的市場售價與時間的函數關系式![]() 寫出圖(2)表示的種植成本與時間的函數關系式
寫出圖(2)表示的種植成本與時間的函數關系式![]()
(2)認定市場售價減去種植成本為純收益,問何時上市的西紅柿收益最大?(注:市場售價和種植成本的單位:元/![]() kg,時間單位:天.)
kg,時間單位:天.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 經過橢圓
經過橢圓![]() :
: ![]() 的左頂點
的左頂點![]() 和上頂點
和上頂點![]() ,橢圓
,橢圓![]() 的右頂點為
的右頂點為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上位于
上位于![]() 軸上方的動點,直線
軸上方的動點,直線![]() 與直線
與直線![]() 分別交于
分別交于![]() 兩點。
兩點。
(1)求橢圓方程;
(2)求線段![]() 的長度的最小值;
的長度的最小值;
(3)當線段![]() 的長度最小時,在橢圓上有兩點
的長度最小時,在橢圓上有兩點![]() ,使得
,使得![]() ,
,![]() 的面積都為
的面積都為![]() ,求直線
,求直線![]() 在y軸上的截距。
在y軸上的截距。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,當![]() 時,
時,![]() ,現已畫出函數在y軸左側的圖象,如圖所示,請根據圖象.
,現已畫出函數在y軸左側的圖象,如圖所示,請根據圖象.

(1)將函數![]() 的圖象補充完整,并寫出函數
的圖象補充完整,并寫出函數![]() 的遞增區間;
的遞增區間;
(2)寫出函數![]() 的解析式;
的解析式;
(3)若函數![]() ,求函數
,求函數![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com