
【題目】已知函數![]() ,
,![]() .
.
(1)若![]() 在
在![]() 處取得極值,求
處取得極值,求![]() 的值;
的值;
(2)設![]() ,試討論函數
,試討論函數![]() 的單調性;
的單調性;
(3)當![]() 時,若存在正實數
時,若存在正實數![]() 滿足
滿足![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() .(2)見解析(3)見解析
.(2)見解析(3)見解析
【解析】
(Ⅰ)由題意,求得函數的導數![]() ,根據
,根據![]() ,即可求解;
,即可求解;
(Ⅱ)由題意,得![]()
![]() ,求得函數的導數
,求得函數的導數![]() ,分類討論,即可求解函數的單調區間;
,分類討論,即可求解函數的單調區間;
(Ⅲ)代入![]() ,求出
,求出![]() ,令
,令![]() ,
,![]() ,根據函數的單調性,即可作出證明.
,根據函數的單調性,即可作出證明.
(1)因為![]() ,所以
,所以![]() ,
,
因為![]() 在
在![]() 處取得極值,
處取得極值,
所以![]() ,解得
,解得![]() .
.
驗證:當![]() 時,
時,![]() 在
在![]() 處取得極大值.
處取得極大值.
(2)解:因為![]()
![]()
所以![]() .
.
①若![]() ,則當
,則當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() ,
,![]() 函數
函數![]() 在
在![]() 上單調遞減.
上單調遞減.
②若![]() ,
,![]() ,
,
當![]() 時,易得函數
時,易得函數![]() 在
在![]() 和
和![]() 上單調遞增,
上單調遞增,
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() 恒成立,所以函數
恒成立,所以函數![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,易得函數
時,易得函數![]() 在
在![]() 和
和![]() 上單調遞增,
上單調遞增,
在![]() 上單調遞減.
上單調遞減.
(3)證明:當![]() 時,
時,![]() ,
,
因為![]() ,
,
所以![]() ,
,
即![]() ,
,
所以![]() .
.
令![]() ,
,![]() ,
,
則![]() ,
,
當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增.
上單調遞增.
所以函數![]() 在
在![]() 時,取得最小值,最小值為
時,取得最小值,最小值為![]() .
.
所以![]() ,
,
即![]() ,所以
,所以![]() 或
或![]() .
.
因為![]() 為正實數,所以
為正實數,所以![]() .
.
當![]() 時,
時,![]() ,此時不存在
,此時不存在![]() 滿足條件,
滿足條件,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】已知圓O:![]() 與直線
與直線![]() 相切.
相切.
(1)求圓O的方程;
(2)若過點![]() 的直線l被圓O所截得的弦長為4,求直線l的方程;
的直線l被圓O所截得的弦長為4,求直線l的方程;
(3)若過點![]() 作兩條斜率分別為
作兩條斜率分別為![]() ,
,![]() 的直線交圓O于B、C兩點,且
的直線交圓O于B、C兩點,且![]() ,求證:直線BC恒過定點.并求出該定點的坐標.
,求證:直線BC恒過定點.并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校組織了一次新高考質量測評,在成績統計分析中,某班的數學成績的莖葉圖和頻率分布直方圖因故都受到不同程度的損壞,但可見部分如下,據此解答如下問題:
5 | 6 | 8 | ||||||||
6 | 2 | 3 | 3 | 5 | 6 | 8 | 9 | |||
7 | 1 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
8 | ||||||||||
9 | 5 | 8 |

(1)求該班數學成績在![]() 的頻率及全班人數;
的頻率及全班人數;
(2)根據頻率分布直方圖估計該班這次測評的數學平均分;
(3)若規定90分及其以上為優秀,現從該班分數在80分及其以上的試卷中任取2份分析學生得分情況,求在抽取的2份試卷中至少有1份優秀的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,F為橢圓C的右焦點.A(-a,0),|AF|=3.
,F為橢圓C的右焦點.A(-a,0),|AF|=3.

(I)求橢圓C的方程;
(II)設O為原點,P為橢圓上一點,AP的中點為M.直線OM與直線x=4交于點D,過O且平行于AP的直線與直線x=4交于點E.求證:∠ODF=∠OEF.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學解答一道解析幾何題:“已知直線l:![]() 與x軸的交點為A,圓O:
與x軸的交點為A,圓O:![]() 經過點A.
經過點A.
(Ⅰ)求r的值;
(Ⅱ)若點B為圓O上一點,且直線AB垂直于直線l,求![]() .”
.”
該同學解答過程如下:
解答:(Ⅰ)令![]() ,即
,即![]() ,解得
,解得![]() ,所以點A的坐標為
,所以點A的坐標為![]() .
.
因為圓O:![]() 經過點A,所以
經過點A,所以![]() .
.
(Ⅱ)因為![]() .所以直線AB的斜率為
.所以直線AB的斜率為![]() .
.
所以直線AB的方程為![]() ,即
,即![]() .
.
代入![]() 消去y整理得
消去y整理得![]() ,
,
解得![]() ,
,![]() .當
.當![]() 時,
時,![]() .所以點B的坐標為
.所以點B的坐標為![]() .
.
所以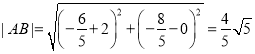 .
.
指出上述解答過程中的錯誤之處,并寫出正確的解答過程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com