
【題目】某校為了普及環保知識,增強學生的環保意識,在全校組織了一次有關環保知識的競賽.經過初賽、復賽,甲、乙兩個代表隊(每隊3人)進入了決賽,規定每人回答一個問題,答對為本隊贏得10分,答錯得0分.假設甲隊中每人答對的概率均為 ![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為 ![]() ,
, ![]() ,
, ![]() ,且各人回答正確與否相互之間沒有影響,用ξ表示乙隊的總得分. (Ⅰ)求ξ的分布列和數學期望;
,且各人回答正確與否相互之間沒有影響,用ξ表示乙隊的總得分. (Ⅰ)求ξ的分布列和數學期望;
(Ⅱ)求甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率.
【答案】解:由題意知,ξ的可能取值為0,10,20,30,
由于乙隊中3人答對的概率分別為 ![]() ,
, ![]() ,
, ![]() ,
,
P(ξ=0)=(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )=
)= ![]() ,
,
P(ξ=10)= ![]() ×(1﹣
×(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )+(1﹣
)+(1﹣ ![]() )×
)× ![]() ×(1﹣
×(1﹣ ![]() )+(1﹣
)+(1﹣ ![]() )×(1﹣
)×(1﹣ ![]() )×
)× ![]() =
= ![]() =
= ![]() ,
,
P(ξ=20)= ![]() ×
× ![]() ×(1﹣
×(1﹣ ![]() )+(1﹣
)+(1﹣ ![]() )×
)× ![]() ×
× ![]() +
+ ![]() ×(1﹣
×(1﹣ ![]() )×
)× ![]() =
= ![]() =
= ![]() ,
,
P(ξ=30)= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
∴ξ的分布列為:
ξ | 0 | 10 | 20 | 30 |
P | | | | |
∴Eξ=0× ![]() +10×
+10× ![]() +20×
+20× ![]() +30×
+30× ![]() =
= ![]() .
.
(Ⅱ)由A表示“甲隊得分等于30乙隊得分等于0”,B表示“甲隊得分等于20乙隊得分等于10”,可知A、B互斥.
又P(A)= ![]() =
= ![]() ,P(B)=
,P(B)= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
則甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率為
P(A+B)=P(A)+P(B)= ![]() =
= ![]() .
.
【解析】(Ⅰ)由題意知,ξ的可能取值為0,10,20,30,分別求出相應的概率,由此能求出ξ的分布列和Eξ;(Ⅱ)由A表示“甲隊得分等于30乙隊得分等于0”,B表示“甲隊得分等于20乙隊得分等于10”,可知A、B互斥.利用互斥事件的概率計算公式即可得出甲、乙兩隊總得分之和等于30分且甲隊獲勝的概率.
【考點精析】利用離散型隨機變量及其分布列對題目進行判斷即可得到答案,需要熟知在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案科目:高中數學 來源: 題型:
【題目】如下圖所示,圓柱的高為2,底面半徑為![]() ,AE、DF是圓柱的兩條母線,過
,AE、DF是圓柱的兩條母線,過![]() 作圓柱的截面交下底面于
作圓柱的截面交下底面于![]() ,四邊形ABCD是正方形.
,四邊形ABCD是正方形.
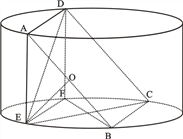
(1)求證![]() ;
;
(2)求四棱錐E-ABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三人獨立破譯同一份密碼.已知三人各自破譯出密碼的概率分別為 ![]() ,且他們是否破譯出密碼互不影響. (Ⅰ)求恰有二人破譯出密碼的概率;
,且他們是否破譯出密碼互不影響. (Ⅰ)求恰有二人破譯出密碼的概率;
(Ⅱ)“密碼被破譯”與“密碼未被破譯”的概率哪個大?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知三棱錐P-ABC,∠ACB=90°,CB=4,AB=20,D為AB的中點,且△PDB是正三角形,PA⊥PC.
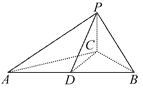
(1)求證:平面PAC⊥平面ABC.
(2)求二面角D-AP-C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】人口問題是當今世界各國普遍關注的問題.認識人口數量的變化規律,可以為有效控制人口增長提供依據.早在1798年,英國經濟學家馬爾薩斯(T.R.Malthus,1766—1834)就提出了自然狀態下的人口增長模型: ![]() ,其中x表示經過的時間,
,其中x表示經過的時間, ![]() 表示x=0時的人口,r表示人口的平均增長率.
表示x=0時的人口,r表示人口的平均增長率.
下表是1950―1959年我國人口數據資料:

如果以各年人口增長率的平均值作為我國這一時期的人口增長率,用馬爾薩斯人口增長模型建立我國這一時期的具體人口增長模型,某同學利用圖形計算器進行了如下探究:
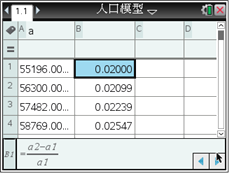
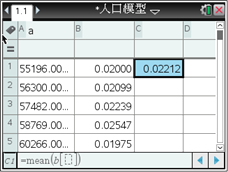
由此可得到我國1950―1959年我國這一時期的具體人口增長模型為____________. (精確到0.001)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知冪函數f(x)=![]() ,其中2<m<2,m∈Z,滿足:
,其中2<m<2,m∈Z,滿足:
(1)f(x)是區間(0,+∞)上的增函數;
(2)對任意的x∈R,都有f(x) +f(x)=0.
求同時滿足條件(1)、(2)的冪函數f(x)的解析式,并求x∈[0,3]時,f(x)的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com