
【題目】如圖,四棱錐![]() 的底面
的底面![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 中點(diǎn).
中點(diǎn).
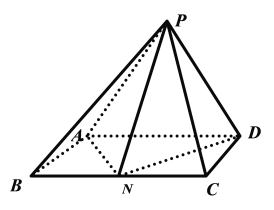
(1)證明:平面![]() 平面
平面![]() ;
;
(2)直線![]() 和平面
和平面![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)可證![]() 平面
平面![]() ,從而得到平面
,從而得到平面![]() 平面
平面![]() .
.
(2)設(shè)![]() 為
為![]() 中點(diǎn),連結(jié)
中點(diǎn),連結(jié)![]() ,
,![]() ,可以證明
,可以證明![]() 、
、![]()
![]() 、
、![]() ,建立如圖所示的空間直角坐標(biāo)系后可求給定的二面角的余弦值.
,建立如圖所示的空間直角坐標(biāo)系后可求給定的二面角的余弦值.
解:(1)∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]()
又∴![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
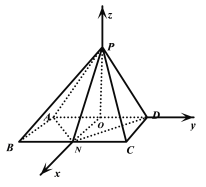
(2)設(shè)![]() 為
為![]() 中點(diǎn),連結(jié)
中點(diǎn),連結(jié)![]() ,
,![]() ,
,
又![]() ,故
,故![]() 且
且![]() ,
,![]() .
.
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]()
![]() ,
,
又![]() 為矩形
為矩形![]() 的對(duì)邊的中點(diǎn),故
的對(duì)邊的中點(diǎn),故![]() .
.
以![]() 為坐標(biāo)原點(diǎn),分別以
為坐標(biāo)原點(diǎn),分別以![]() 為
為![]() 軸正方向建立空間直角坐標(biāo)系,
軸正方向建立空間直角坐標(biāo)系,
則![]() ,
,![]() .
.
設(shè)![]() ,其中
,其中![]() ,則
,則![]() .
.
又平面![]() 的法向量為
的法向量為![]() ,
,
所以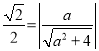 ,故
,故![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() .
.
故![]() ,
,![]() ,
,![]() ,
,
設(shè)平面![]() 的法向量為
的法向量為![]()
故 即
即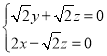 ,
,
令![]() ,∴
,∴![]() .
.
設(shè)平面![]() 的法向量為
的法向量為![]()
故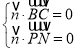 即
即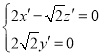 ,
,
令![]() ,∴
,∴![]() ,
,
∴![]() ,
,
因?yàn)槎娼?/span>![]() 為銳角,故其余弦值為
為銳角,故其余弦值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若不等式![]() 區(qū)間
區(qū)間![]() 上恒成立,求實(shí)數(shù)
上恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)求證: ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】北極冰融是近年來最引人注目的氣候變化現(xiàn)象之一白色冰面融化變成顏色相對(duì)較暗的海冰,被稱為“北極變暗”現(xiàn)象,21世紀(jì)以來,北極的氣溫變化是全球平均水平的2倍,被稱為“北極放大”現(xiàn)象.如圖為北極年平均海冰面積(![]() )與年平均
)與年平均![]()
![]() 濃度圖.則下列說法正確的是( )
濃度圖.則下列說法正確的是( )
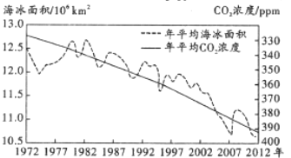
A.北極年海冰面積逐年減少
B.北極年海冰面積減少速度不斷加快
C.北極年海冰面積與年平均二氧化碳濃度大體成負(fù)相關(guān)
D.北極年海冰面積與年平均二氧化碳濃度大體成正相關(guān)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
, ![]() ,點(diǎn)F為棱
,點(diǎn)F為棱![]() 的中點(diǎn),點(diǎn)E為線段
的中點(diǎn),點(diǎn)E為線段![]() 上的動(dòng)點(diǎn).
上的動(dòng)點(diǎn).
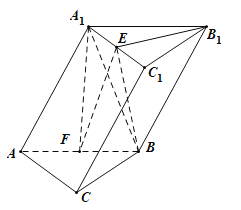
(1)求證:![]() ;
;
(2)若點(diǎn)E為線段![]() 的中點(diǎn),求點(diǎn)C到平面
的中點(diǎn),求點(diǎn)C到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】遼寧省六校協(xié)作體(葫蘆島第一高中、東港二中、鳳城一中、北鎮(zhèn)高中、瓦房店高中、丹東四中)中的某校文科實(shí)驗(yàn)班的![]() 名學(xué)生期中考試的語文、數(shù)學(xué)成績都不低于
名學(xué)生期中考試的語文、數(shù)學(xué)成績都不低于![]() 分,其中語文成績的頻率分布直方圖如圖所示,成績分組區(qū)間是:
分,其中語文成績的頻率分布直方圖如圖所示,成績分組區(qū)間是:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
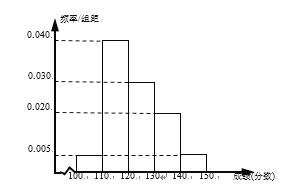
(1)根據(jù)頻率分布直方圖,估計(jì)這![]() 名學(xué)生語文成績的中位數(shù)和平均數(shù);(同一組數(shù)據(jù)用該區(qū)間的中點(diǎn)值作代表;中位數(shù)精確到
名學(xué)生語文成績的中位數(shù)和平均數(shù);(同一組數(shù)據(jù)用該區(qū)間的中點(diǎn)值作代表;中位數(shù)精確到![]() )
)
(2)若這![]() 名學(xué)生語文成績某些分?jǐn)?shù)段的人數(shù)
名學(xué)生語文成績某些分?jǐn)?shù)段的人數(shù)![]() 與數(shù)學(xué)成績相應(yīng)分?jǐn)?shù)段的人數(shù)
與數(shù)學(xué)成績相應(yīng)分?jǐn)?shù)段的人數(shù)![]() 之比如下表所示:
之比如下表所示:
分組區(qū)間 |
|
|
|
|
|
|
|
|
|
從數(shù)學(xué)成績在![]() 的學(xué)生中隨機(jī)選取
的學(xué)生中隨機(jī)選取![]() 人,求選出的
人,求選出的![]() 人中恰好有
人中恰好有![]() 人數(shù)學(xué)成績在
人數(shù)學(xué)成績在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知四邊形![]() 是梯形(如圖1),
是梯形(如圖1),![]() ,
,![]() ,
,![]() ,
,![]() ,E為
,E為![]() 的中點(diǎn),以
的中點(diǎn),以![]() 為折痕把
為折痕把![]() 折起,使點(diǎn)D到達(dá)點(diǎn)P的位置(如圖2),且
折起,使點(diǎn)D到達(dá)點(diǎn)P的位置(如圖2),且![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求點(diǎn)C到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 為
為![]() 上一點(diǎn)且
上一點(diǎn)且![]() =
=![]() =
=![]() =
=![]() .
.
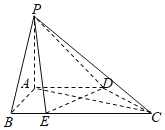
(1)求證:平面![]() 平面
平面![]() ;
;
(2)若直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】“新冠肺炎”疫情的控制需要根據(jù)大數(shù)據(jù)進(jìn)行分析,并有針對(duì)性的采取措施.下圖是甲、乙兩個(gè)省份從2月7日到2月13日一周內(nèi)的新增“新冠肺炎”確診人數(shù)的折線圖.根據(jù)圖中甲、乙兩省的數(shù)字特征進(jìn)行比對(duì),下列說法錯(cuò)誤的是( )
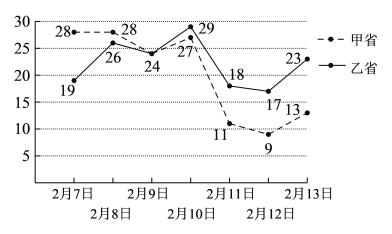
A.2月7日到2月13日甲省的平均新增“新冠肺炎”確診人數(shù)低于乙省
B.2月7日到2月13日甲省的單日新增“新冠肺炎”確診人數(shù)最大值小于乙省
C.2月7日到2月13日乙省相對(duì)甲省的新增“新冠甲省肺炎”確診人數(shù)的波動(dòng)大
D.后四日(2月10日至13日)乙省每日新增“新冠肺炎”確診人數(shù)均比甲省多
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com