
 <t<1,則a+b的值不可能是
<t<1,則a+b的值不可能是
 <t<1時的取值情況,然后進行討論即可.
<t<1時的取值情況,然后進行討論即可. ,x=0,x=
,x=0,x= ,若g(x)=0,則x有3個解,不妨設為x=n,x=0,x=-n,(0<n<1)
,若g(x)=0,則x有3個解,不妨設為x=n,x=0,x=-n,(0<n<1) ,或g(x)-t=0,或g(x)-t=-
,或g(x)-t=0,或g(x)-t=- ,.
,. ,或g(x)=t,或g(x)=t-
,或g(x)=t,或g(x)=t- .
. <t<1時,由g(x)=t,得x有3個解.
<t<1時,由g(x)=t,得x有3個解.
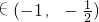 ,此時x有3個解.
,此時x有3個解.
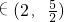 ,此時方程無解.所以a=3+3=6.
,此時方程無解.所以a=3+3=6. <t<1,所以此時x有4個解.
<t<1,所以此時x有4個解. <t<1,0<n<1,所以若0<n<
<t<1,0<n<1,所以若0<n< ,則
,則 <t+n<
<t+n< ,此時x有4個解或2解或0個解.
,此時x有4個解或2解或0個解.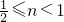 ,則1<t+n<2,此時x無解.對應f(x)=t-n∈(
,則1<t+n<2,此時x無解.對應f(x)=t-n∈(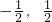 ),對應的有2個解或3解或4個解.
),對應的有2個解或3解或4個解.

 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |

查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省菏澤市鄆城一中高三(上)第一次診斷數學試卷(理科)(解析版) 題型:選擇題
查看答案和解析>>
科目:高中數學 來源:2010年山東省菏澤市鄆城一中高考數學一模試卷(理科)(解析版) 題型:選擇題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com