
【題目】某地合作農場的果園進入盛果期,果農利用互聯網電商渠道銷售蘋果,蘋果單果直徑不同則單價不同,為了更好的銷售,現從該合作農場果園的蘋果樹上隨機摘下了50個蘋果測量其直徑,經統計,其單果直徑分布在區間![]() 內(單位:
內(單位:![]() ),統計的莖葉圖如圖所示:
),統計的莖葉圖如圖所示:

(Ⅰ)按分層抽樣的方法從單果直徑落在![]() ,
,![]() 的蘋果中隨機抽取6個,則從
的蘋果中隨機抽取6個,則從![]() ,
,![]() 的蘋果中各抽取幾個?
的蘋果中各抽取幾個?
(Ⅱ)從(Ⅰ)中選出的6個蘋果中隨機抽取2個,求這兩個蘋果單果直徑均在![]() 內的概率;
內的概率;
(Ⅲ)以此莖葉圖中單果直徑出現的頻率代表概率,若該合作農場的果園有20萬個蘋果約5萬千克待出售,某電商提出兩種收購方案:方案![]() :所有蘋果均以5.5元/千克收購;方案
:所有蘋果均以5.5元/千克收購;方案![]() :按蘋果單果直徑大小分3類裝箱收購,每箱裝25個蘋果,定價收購方式為:單果直徑在
:按蘋果單果直徑大小分3類裝箱收購,每箱裝25個蘋果,定價收購方式為:單果直徑在![]() 內按35元/箱收購,在
內按35元/箱收購,在![]() 內按45元/箱收購,在
內按45元/箱收購,在![]() 內按55元/箱收購.包裝箱與分揀裝箱費用為5元/箱(該費用由合作農場承擔).請你通過計算為該合作農場推薦收益最好的方案.
內按55元/箱收購.包裝箱與分揀裝箱費用為5元/箱(該費用由合作農場承擔).請你通過計算為該合作農場推薦收益最好的方案.
【答案】(Ⅰ)4個;(Ⅱ)![]() ;(Ⅲ)方案是
;(Ⅲ)方案是![]()
【解析】
(Ⅰ)單果直徑落在![]() ,
,![]() ,
,![]() ,
,![]() 的蘋果個數分別為6,12,分層抽樣的方法從單果直徑落在
的蘋果個數分別為6,12,分層抽樣的方法從單果直徑落在![]() ,
,![]() ,
,![]() ,
,![]() 的蘋果中隨機抽取6個,單果直徑落在
的蘋果中隨機抽取6個,單果直徑落在![]() ,
,![]() ,
,![]() ,
,![]() 的蘋果分別抽取2個和4個;(Ⅱ)從這6個蘋果中隨機抽取2個,基本事件總數
的蘋果分別抽取2個和4個;(Ⅱ)從這6個蘋果中隨機抽取2個,基本事件總數![]() ,這兩個蘋果單果直徑均在
,這兩個蘋果單果直徑均在![]() ,
,![]() 內包含的基本事件個數
內包含的基本事件個數![]() ,由此能求出這兩個蘋果單果直徑均在
,由此能求出這兩個蘋果單果直徑均在![]() ,
,![]() 內的概率;(Ⅲ)分別求出按方案
內的概率;(Ⅲ)分別求出按方案![]() 與方案
與方案![]() 該合作農場收益,比較大小得結論.
該合作農場收益,比較大小得結論.
(Ⅰ)由莖葉圖可知,單果直徑落在![]() ,
,![]() 的蘋果分別為6個,12個,
的蘋果分別為6個,12個,
依題意知抽樣比為![]() ,所以單果直徑落在
,所以單果直徑落在![]() 的蘋果抽取個數為
的蘋果抽取個數為![]() 個,
個,
單果直徑落在![]() 的蘋果抽取個數為
的蘋果抽取個數為![]() 個
個
(Ⅱ)記單果直徑落在![]() 的蘋果為
的蘋果為![]() ,
,![]() ,記單果直徑落在
,記單果直徑落在![]() 的蘋果為
的蘋果為![]() ,若從這6個蘋果中隨機抽取2個,則所有可能結果為:
,若從這6個蘋果中隨機抽取2個,則所有可能結果為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,即基本事件的總數為15個.
,即基本事件的總數為15個.
這兩個蘋果單果直徑均落在![]() 內包含的基本事件個數為6個,
內包含的基本事件個數為6個,
所以這兩個蘋果單果直徑均落在![]() 內的概率為
內的概率為![]() .
.
(Ⅲ)按方案![]() :該合作農場收益為:
:該合作農場收益為:![]() (萬元);
(萬元);
按方案![]() :依題意可知合作農場的果園共有
:依題意可知合作農場的果園共有![]() 萬箱,即8000箱蘋果,
萬箱,即8000箱蘋果,
則該合作農場收益為:![]() 元,
元,
即為31.36萬元 因為![]() ,
,
所以為該合作農場推薦收益最好的方案是![]() .
.


科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知2cosC(acosB+bcosA)=c.
(1)求C;
(2)若c= ![]() ,△ABC的面積為
,△ABC的面積為 ![]() ,求△ABC的周長.
,求△ABC的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市交通部門為了對該城市共享單車加強監管,隨機選取了100人就該城市共享單車的推行情況進行問卷調查,并將問卷中的這100人根據其滿意度評分值(百分制)按照![]() ,
,![]() ,
,![]() ,
,![]() 分成5組,制成如圖所示頻率分直方圖.
分成5組,制成如圖所示頻率分直方圖.

(1)求圖中x的值;
(2)求這組數據的平均數和中位數;
(3)已知滿意度評分值在![]() 內的男生數與女生數的比為
內的男生數與女生數的比為![]() ,若在滿意度評分值為
,若在滿意度評分值為![]() 的人中隨機抽取2人進行座談,求2人均為男生的概率.
的人中隨機抽取2人進行座談,求2人均為男生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
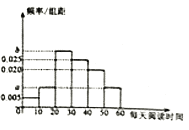
【題目】某校為了了解學生每天平均課外閱讀的時間(單位:分鐘),從本校隨機抽取了100名學生進行調查,根據收集的數據,得到學生每天課外閱讀時間的頻率分布直方圖,如圖所示,若每天課外閱讀時間不超過30分鐘的有45人.
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)根據頻率分布直方圖,估計該校學生每天課外閱讀時間的中位數及平均值(同一組中的數據用該組區間的中點值代表).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的定義域為A,若
的定義域為A,若![]() 時總有
時總有![]() 為單函數.例如,函數
為單函數.例如,函數![]() =2x+1(
=2x+1(![]() )是單函數.下列命題:
)是單函數.下列命題:
①函數![]() =
=![]() (x
(x![]() R)是單函數;②若
R)是單函數;②若![]() 為單函數,
為單函數,![]() 且
且![]() 則
則![]() ;③若f:A
;③若f:A![]() B為單函數,則對于任意b
B為單函數,則對于任意b![]() B,它至多有一個原象;
B,它至多有一個原象;
④函數f(x)在某區間上具有單調性,則f(x)一定是單函數.其中的真命題是 .(寫出所有真命題的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題a2x2+ax﹣2=0在[﹣1,1]上有解;命題q:只有一個實數x滿足不等式x2+2ax+2a≤0,若命題“p”或“q”是假命題,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)在定義域[-1,1]上既是奇函數,又是減函數.
(1)求證:對任意x1,x2∈[-1,1],有[f(x1)+f(x2)]·(x1+x2)≤0;
(2)若f(1-a)+f(1-a2)<0,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓C: ![]() (a>2
(a>2 ![]() )的右焦點為F,右頂點為A,上頂點為B,且滿足
)的右焦點為F,右頂點為A,上頂點為B,且滿足 ![]() ,其中O 為坐標原點,e為橢圓的離心率.
,其中O 為坐標原點,e為橢圓的離心率.
(1)求橢圓C的方程;
(2)設點P是橢圓C上一點,直線PA與y軸交于點M,直線PB與x軸交于點N,求證:|AN||BM|為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com