
【題目】已知![]() 兩點分別在
兩點分別在![]() 軸和
軸和![]() 軸上運動,且
軸上運動,且![]() ,若動點
,若動點![]() 滿足
滿足![]() .
.
(1)求出動點![]() 的軌跡
的軌跡![]() 的標準方程;
的標準方程;
(2)設動直線![]() 與曲線
與曲線![]() 有且僅有一個公共點,與圓
有且僅有一個公共點,與圓![]() 相交于兩點
相交于兩點![]() (兩點均不在坐標軸上),求直線
(兩點均不在坐標軸上),求直線![]() 的斜率之積.
的斜率之積.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,底面ABCD為正方形,平面PAD⊥平面ABCD,點M在線段PPD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求證:M為PB的中點;
(II)求二面角B-PD-A的大小;
(III)求直線MC與平面BDP所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】到2020年,我國將全面建立起新的高考制度,新高考采用![]() 模式,其中語文、數學、英語三科為必考科目,滿分各150分,另外考生還要依據想考取的高校及專業的要求,結合自己的興趣、愛好等因素,在思想政治、歷史、地理、物理、化學、生物6門科目中自選3門(6選3)參加考試,滿分各100分.為了順利迎接新高考改革,某學校采用分層抽樣的方法從高一年級1000名(其中男生550名,女生450名)學生中抽取了
模式,其中語文、數學、英語三科為必考科目,滿分各150分,另外考生還要依據想考取的高校及專業的要求,結合自己的興趣、愛好等因素,在思想政治、歷史、地理、物理、化學、生物6門科目中自選3門(6選3)參加考試,滿分各100分.為了順利迎接新高考改革,某學校采用分層抽樣的方法從高一年級1000名(其中男生550名,女生450名)學生中抽取了![]() 名學生進行調查.
名學生進行調查.
(1)已知抽取的![]() 名學生中有女生45名,求
名學生中有女生45名,求![]() 的值及抽取的男生的人數.
的值及抽取的男生的人數.
(2)該校計劃在高一上學期開設選修中的“物理”和“地理”兩個科目,為了解學生對這兩個科目的選課情況,對在(1)的條件下抽取到的![]() 名學生進行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目,且只能選擇一個科目),得到如下
名學生進行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目,且只能選擇一個科目),得到如下![]() 列聯表.
列聯表.
選擇“物理” | 選擇“地理” | 總計 | |
男生 | 10 | ||
女生 | 25 | ||
總計 |
(i)請將列聯表補充完整,并判斷是否有![]() 以上的把握認為選擇科目與性別有關系.
以上的把握認為選擇科目與性別有關系.
(ii)在抽取的選擇“地理”的學生中按性別分層抽樣抽取6名,再從這6名學生中抽取2名,求這2名中至少有1名男生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《張丘建算經》是中國古代的著名數學著作,該書表明:至遲于公元5世紀,中國已經系統掌握等差數列的相關理論,該書上卷22題又“女工善織問題”:“今有女善織,日益功疾,初日織五尺,今一月曰織九匹三丈,問日益幾何?”,大概意思是:有一個女工人善于織布,每天織布的尺數越來越多且成等差數列,第一天知5尺,30天共織九匹三丈,問每天增加的織布數目是多少寸?答案是__________寸.(注:當時一匹為四丈,一丈為十尺,一尺為十寸,結果四舍五入精確到寸)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,原點為
中,原點為![]() ,拋物線
,拋物線![]() 的方程為
的方程為![]() ,線段
,線段![]() 是拋物線
是拋物線![]() 的一條動弦.
的一條動弦.
(1)求拋物線![]() 的準線方程和焦點坐標
的準線方程和焦點坐標![]() ;
;
(2)當![]() 時,設圓
時,設圓![]() :
:![]() ,若存在兩條動弦
,若存在兩條動弦![]() ,滿足直線
,滿足直線![]() 與圓
與圓![]() 相切,求半徑
相切,求半徑![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C的參數方程為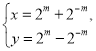 (m為參數),以O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
(m為參數),以O為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為![]() ρcosθ
ρcosθ![]() ρsinθ
ρsinθ![]() 2
2![]() =0.
=0.
(1)求C和l的直角坐標方程;
(2)設直線l與曲線C的公共點為P,Q,求|PQ|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場一年中各月份的收入、支出情況的統計如圖所示,下列說法中正確的是______.
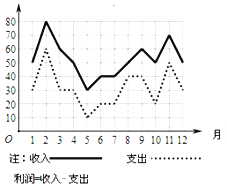
①2至3月份的收入的變化率與11至12月份的收入的變化率相同;
②支出最高值與支出最低值的比是6:1;
③第三季度平均收入為50萬元;
④利潤最高的月份是2月份。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com