分析:(1)過A作AQ∥C
1N,交A
1C
1于Q,連接B
1Q,可得∠B
1AQ(或其補角)是異面直線AB
1與C
1N所成角.在△B
1AQ中,分別求出AB
1、AQ和B
1Q的長,結合余弦定理算出cos∠B
1AQ的值,從而得到異面直線AB
1與C
1N所成的角是arccos
;
(2)平面A
1B
1C
1中,過M作MH⊥A
1C
1于H.根據直三棱柱的性質結合面面垂直的性質定理,得到MH⊥平面AA
1C
1C,MH是三棱錐M-C
1CN的高.算出MH的長和△C
1CN的面積,結合三棱錐的體積公式,可得三棱錐M-C
1CN的體積.
解答:解:(1)平面AA
1C
1C中,過A作AQ∥C
1N,交A
1C
1于Q,連接B
1Q
∴∠B
1AQ(或其補角)就是異面直線AB
1與C
1N所成的角

矩形AA
1C
1C中,N是AC中點,可得Q是A
1C
1中點
Rt△AA
1B
1中,AB
1=
=5,同理可得AQ=
∵等腰Rt△A
1B
1C
1中,B
1Q是斜邊的中線
∴B
1Q=
A
1B
1=2
,
△B
1AQ中,cos∠B
1AQ=
=
>0
∴∠B
1AQ=arccos
,即異面直線AB
1與C
1N所成的角等于arccos
;
(2)平面A
1B
1C
1中,過M作MH⊥A
1C
1于H
∵直三棱柱ABC-A
1B
1C
1中,CC
1⊥平面A
1B
1C
1,CC
1⊆平面AA
1C
1C
∴平面AA
1C
1C⊥平面A
1B
1C
1,
∵平面AA
1C
1C⊥平面A
1B
1C
1=A
1C
1,MH⊥A
1C
1,
∴MH⊥平面AA
1C
1C,MH是三棱錐M-C
1CN的高線
∵△B
1C
1Q中,M是B
1C
1中點,MH∥B
1Q
∴MH是△B
1C
1Q的中位線,得MH=
B
1Q=
∵△C
1CN的面積S=
CN×C
1C=
×2
×3=3
∴三棱錐M-C
1CN的體積V
M-C1CN=
S
C1CN×MH=
×3
×
=2
點評:本題給出特殊三棱柱,求異面直線所成角并求錐體的體積,著重考查了線面垂直、面面垂直的判定與性質,異面直線所成角的求法和錐體體積公式等知識,屬于基礎題.

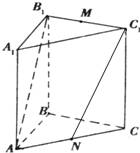 (2012•香洲區模擬)如圖,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分別是B1C1和AC的中點.
(2012•香洲區模擬)如圖,直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=4,BC=4,BB1=3,M、N分別是B1C1和AC的中點.


