
【題目】如圖,三棱柱![]() 中,側面
中,側面![]() 為菱形,
為菱形,![]() .
.

(1)證明:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
科目:高中數學 來源: 題型:
【題目】△ABC的角A、B、C的對邊分別為a、b、c,![]() =(2b-c,a),
=(2b-c,a),![]() =(cosA,-cosC),且
=(cosA,-cosC),且![]() ⊥
⊥![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)當y=2sin2B+sin(2B+![]() )取最大值時,求角
)取最大值時,求角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設經過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點,經過點
兩點,經過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 相切于點
相切于點![]() .
.
(1)當![]() 時,求
時,求![]() 的取值范圍;
的取值范圍;
(2)問是否存在直線![]() ,
,![]() 使得
使得![]() 成立,若存在,求出
成立,若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P-ABC中,已知![]() ,頂點P在平面ABC上的射影為
,頂點P在平面ABC上的射影為![]() 的外接圓圓心.
的外接圓圓心.
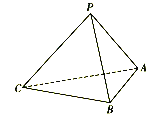
(1)證明:平面![]() 平面ABC;
平面ABC;
(2)若點M在棱PA上,![]() ,且二面角P-BC-M的余弦值為
,且二面角P-BC-M的余弦值為![]() ,試求
,試求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,A、B為橢圓C:![]() 短軸的上、下頂點,P為直線l:y=2上一動點,連接PA并延長交橢圓于點M,連接PB交橢圓于點N,已知直線MA,MB的斜率之積恒為
短軸的上、下頂點,P為直線l:y=2上一動點,連接PA并延長交橢圓于點M,連接PB交橢圓于點N,已知直線MA,MB的斜率之積恒為![]() .
.

(1)求橢圓C的標準方程;
(2)若直線MN與x軸平行,求直線MN的方程;
(3)求四邊形AMBN面積的最大值,并求對應的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某印刷廠為了研究單冊書籍的成本![]() (單位:元)與印刷冊數
(單位:元)與印刷冊數![]() (單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:
(單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:
印刷冊數 |
|
|
|
|
|
單冊成本 |
|
|
|
|
|
根據以上數據,技術人員分別借助甲、乙兩種不同的回歸模型,得到兩個回歸方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)為了評價兩種模型的擬合效果,完成以下任務.
①完成下表(計算結果精確到![]() );
);
印刷冊數 |
|
|
|
|
| |
單冊成本 |
|
|
|
|
| |
模型甲 | 估計值 |
|
|
| ||
殘差 |
|
|
| |||
模型乙 | 估計值 |
|
|
| ||
殘差 |
|
|
| |||
②分別計算模型甲與模型乙的殘差平方和,并通過比較,判斷哪個模型擬合效果更好.
(2)該書上市之后,受到廣大讀者熱烈歡迎,不久便全部售罄,于是印刷廠決定進行二次印刷,根據市場調查,新需求量為![]() 千冊,若印刷廠以每冊
千冊,若印刷廠以每冊![]() 元的價格將書籍出售給訂貨商,求印刷廠二次印刷
元的價格將書籍出售給訂貨商,求印刷廠二次印刷![]() 千冊獲得的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本).
千冊獲得的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國改革開放以來經濟發展迅猛,某一線城市的城鎮居民2012~2018年人均可支配月收入散點圖如下(年份均用末位數字減1表示).
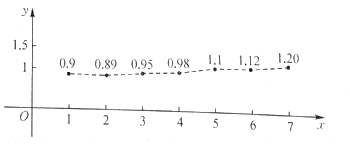
(1)由散點圖可知,人均可支配月收入y(萬元)與年份x之間具有較強的線性相關關系,試求y關于x的回歸方程(系數精確到0.001),依此相關關系預測2019年該城市人均可支配月收入;
(2)在2014~2018年的五個年份中隨機抽取兩個數據作樣本分析,求所取的兩個數據中,人均可支配月收入恰好有一個超過1萬元的概率.
注: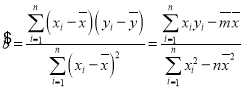 ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com