
【題目】已知橢圓![]() 的兩個(gè)焦點(diǎn)分別為
的兩個(gè)焦點(diǎn)分別為![]() ,短軸的兩個(gè)端點(diǎn)分別為
,短軸的兩個(gè)端點(diǎn)分別為![]() .
.
(Ⅰ)若![]() 為等邊三角形,求橢圓
為等邊三角形,求橢圓![]() 的方程;
的方程;
(Ⅱ)若橢圓![]() 的短軸長(zhǎng)為
的短軸長(zhǎng)為![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 的直線(xiàn)
的直線(xiàn)![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,求直線(xiàn)
,求直線(xiàn)![]() 的方程.
的方程.
【答案】(Ⅰ)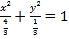 ;(Ⅱ)
;(Ⅱ)![]() 或
或![]() .
.
【解析】試題分析:(1)由![]() 為等邊三角形可得a=2b,又c=1,集合
為等邊三角形可得a=2b,又c=1,集合![]() 可求
可求![]() ,則橢圓C的方程可求;(2)由給出的橢圓C的短軸長(zhǎng)為2,結(jié)合c=1求出橢圓方程,分過(guò)點(diǎn)F2的直線(xiàn)l的斜率存在和不存在討論,當(dāng)斜率存在時(shí),把直線(xiàn)方程和橢圓方程聯(lián)立,由根與系數(shù)關(guān)系寫(xiě)出兩個(gè)交點(diǎn)的橫坐標(biāo)的和,把
,則橢圓C的方程可求;(2)由給出的橢圓C的短軸長(zhǎng)為2,結(jié)合c=1求出橢圓方程,分過(guò)點(diǎn)F2的直線(xiàn)l的斜率存在和不存在討論,當(dāng)斜率存在時(shí),把直線(xiàn)方程和橢圓方程聯(lián)立,由根與系數(shù)關(guān)系寫(xiě)出兩個(gè)交點(diǎn)的橫坐標(biāo)的和,把
![]() 轉(zhuǎn)化為數(shù)量積等于0,代入坐標(biāo)后可求直線(xiàn)的斜率,則直線(xiàn)l的方程可求
轉(zhuǎn)化為數(shù)量積等于0,代入坐標(biāo)后可求直線(xiàn)的斜率,則直線(xiàn)l的方程可求
試題解析:(1)![]() 為等邊三角形,則
為等邊三角形,則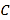 ……2
……2
橢圓![]() 的方程為:
的方程為: ![]() ; ……3
; ……3
(2)容易求得橢圓![]() 的方程為
的方程為![]() , ……5
, ……5
當(dāng)直線(xiàn)![]() 的斜率不存在時(shí),其方程為
的斜率不存在時(shí),其方程為![]() ,不符合題意; ……6
,不符合題意; ……6
當(dāng)直線(xiàn)的斜率存在時(shí),設(shè)直線(xiàn)![]() 的方程為
的方程為![]() ,
,
由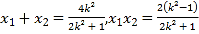 得
得![]() ,設(shè)
,設(shè)![]() ,
,
則![]() , ……8
, ……8
![]() ∵
∵![]() ,
,
∴![]() ,
,
即![]()
![]() ……10
……10
解得![]() ,即
,即![]() ,
,
故直線(xiàn)![]() 的方程為
的方程為![]() 或
或![]() . ……12
. ……12



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】學(xué)校為了了解高三學(xué)生每天自主學(xué)習(xí)中國(guó)古典文學(xué)的時(shí)間,隨機(jī)抽取了高三男生和女生各50名進(jìn)行問(wèn)卷調(diào)查,其中每天自主學(xué)習(xí)中國(guó)古典文學(xué)的時(shí)間超過(guò)3小時(shí)的學(xué)生稱(chēng)為“古文迷”,否則為“非古文迷”,調(diào)查結(jié)果如表:
古文迷 | 非古文迷 | 合計(jì) | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合計(jì) | 56 | 44 | 100 |
(Ⅰ)根據(jù)表中數(shù)據(jù)能否判斷有![]() 的把握認(rèn)為“古文迷”與性別有關(guān)?
的把握認(rèn)為“古文迷”與性別有關(guān)?
(Ⅱ)現(xiàn)從調(diào)查的女生中按分層抽樣的方法抽出5人進(jìn)行調(diào)查,求所抽取的5人中“古文迷”和“非古文迷”的人數(shù);
(Ⅲ)現(xiàn)從(Ⅱ)中所抽取的5人中再隨機(jī)抽取3人進(jìn)行調(diào)查,記這3人中“古文迷”的人數(shù)為![]() ,求隨機(jī)變量
,求隨機(jī)變量![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
參考公式:  ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0;
(2)b為何值時(shí),ax2+bx+3≥0的解集為R.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,以原點(diǎn)為圓心,橢圓C的短半軸長(zhǎng)為半徑的圓與直線(xiàn)
,以原點(diǎn)為圓心,橢圓C的短半軸長(zhǎng)為半徑的圓與直線(xiàn)![]() 相切.
相切.![]() 、
、![]() 是橢圓的左、右頂點(diǎn),直線(xiàn)
是橢圓的左、右頂點(diǎn),直線(xiàn)![]() 過(guò)
過(guò)![]() 點(diǎn)且與
點(diǎn)且與![]() 軸垂直.
軸垂直.
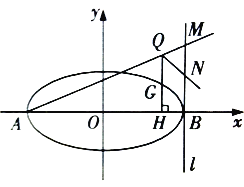
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 、
、![]() 的任意一點(diǎn),作
的任意一點(diǎn),作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,延長(zhǎng)
,延長(zhǎng)![]() 到點(diǎn)
到點(diǎn)![]() 使得
使得![]() ,連接
,連接![]() 并延長(zhǎng)交直線(xiàn)
并延長(zhǎng)交直線(xiàn)![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 為線(xiàn)段
為線(xiàn)段![]() 的中點(diǎn),判斷直線(xiàn)
的中點(diǎn),判斷直線(xiàn)![]() 與以
與以![]() 為直徑的圓
為直徑的圓![]() 的位置關(guān)系,并證明你的結(jié)論.
的位置關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,以原點(diǎn)為圓心,橢圓C的短半軸長(zhǎng)為半徑的圓與直線(xiàn)
,以原點(diǎn)為圓心,橢圓C的短半軸長(zhǎng)為半徑的圓與直線(xiàn)![]() 相切.
相切.![]() 、
、![]() 是橢圓的左、右頂點(diǎn),直線(xiàn)
是橢圓的左、右頂點(diǎn),直線(xiàn)![]() 過(guò)
過(guò)![]() 點(diǎn)且與
點(diǎn)且與![]() 軸垂直.
軸垂直.

(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)![]() 是橢圓
是橢圓![]() 上異于
上異于![]() 、
、![]() 的任意一點(diǎn),作
的任意一點(diǎn),作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,延長(zhǎng)
,延長(zhǎng)![]() 到點(diǎn)
到點(diǎn)![]() 使得
使得![]() ,連接
,連接![]() 并延長(zhǎng)交直線(xiàn)
并延長(zhǎng)交直線(xiàn)![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 為線(xiàn)段
為線(xiàn)段![]() 的中點(diǎn),判斷直線(xiàn)
的中點(diǎn),判斷直線(xiàn)![]() 與以
與以![]() 為直徑的圓
為直徑的圓![]() 的位置關(guān)系,并證明你的結(jié)論.
的位置關(guān)系,并證明你的結(jié)論.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() ,
, ![]() 取一切非負(fù)實(shí)數(shù)時(shí),若
取一切非負(fù)實(shí)數(shù)時(shí),若![]() ,求
,求![]() 的范圍;
的范圍;
(2)若函數(shù)![]() 存在極大值
存在極大值![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知直線(xiàn)l與圓C:x2+y2+2x﹣4y+a=0相交于A(yíng),B兩點(diǎn),弦AB的中點(diǎn)為M(0,1).
(1)若圓C的半徑為![]() ,求實(shí)數(shù)a的值;
,求實(shí)數(shù)a的值;
(2)若弦AB的長(zhǎng)為6,求實(shí)數(shù)a的值;
(3)當(dāng)a=1時(shí),圓O:x2+y2=2與圓C交于M,N兩點(diǎn),求弦MN的長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知過(guò)拋物線(xiàn)y2=2px(p>0)的焦點(diǎn),斜率為2![]() 的直線(xiàn)交拋物線(xiàn)于A(yíng)(x1,y1),B(x2,y2)(x1<x2)兩點(diǎn),且|AB|=9.
的直線(xiàn)交拋物線(xiàn)于A(yíng)(x1,y1),B(x2,y2)(x1<x2)兩點(diǎn),且|AB|=9.
(1)求該拋物線(xiàn)的方程.
(2)O為坐標(biāo)原點(diǎn),C為拋物線(xiàn)上一點(diǎn),若![]() ,求λ的值
,求λ的值
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在![]() 中,
中, ![]() 成等差數(shù)列是
成等差數(shù)列是![]() 的( )
的( )
A. 充分不必要條件 B. 必要不充分條件 C. 充要條件 D. 既不充分也不必要條件
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com