免费电影视频在线看,久草视频视频在线播放,欧美一区二区三区

精英家教網 > 高中數學 > 題目詳情

【題目】在中，角的對邊分別為，且，若的面積為，則的最小值為（）

A.B.C.D.3

【答案】B

【解析】

試題由正弦定理，有，又2c·cosB＝2a＋b，得

2sinC·cosB＝2sin A＋sinB，

由A＋B＋C＝π，得sin A＝sin(B＋C)，

則2sinC·cosB＝2sin(B＋C)＋sinB，即2sinB·cosC＋sinB＝0，

又0＜B＜π，sinB＞0，得cosC＝－，

因為0＜C＜π，得C＝，

則△ABC的面積為S△＝ab sinC＝ab，即c＝3ab，

由余弦定理，得c2＝a2＋b2－2ab cosC，化簡，得a2＋b2＋ab＝9a2b2，

∵a2＋b2≥2ab，當僅當a=b時取等號，

∴2ab＋ab≤9a2b2，即ab≥，故ab的最小值是．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】動點到定點的距離比它到直線的距離小1，設動點的軌跡為曲線，過點的直線交曲線于、兩個不同的點，過點、分別作曲線的切線，且二者相交于點.

（1）求曲線的方程；

（2）求證：；

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知A、B是單位圓O上的兩點（O為圓心），∠AOB=120°，點C是線段AB上不與A、B重合的動點.MN是圓O的一條直徑，則的取值范圍是（）

A. [，0） B. [，0] C. [，1） D. [，1]

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數在區間上有最大值和最小值.設

（1）求的值

（2）若不等式在上有解,求實數的取值范圍;

（3）若有三個不同的實數解,求實數的取值范圍.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】設數列{an}滿足：①a1=1；②所有項an∈N*；③1=a1<a2<…<an<an+1<….設集合Am={n|an≤m，m∈N*），將集合Am中的元素的最大值記為bm，即bm是數列{an}中滿足不等式an≤m的所有項的項數的最大值.我們稱數列{bn}為數列{an}的伴隨數列.

例如，數列1，3，5的伴隨數列為1，1，2，2，3.

（I）若數列{an}的伴隨數列為1，1，2，2，2，3，3，3，3……，請寫出數列{an}；

（II）設an=4n-1，求數列{an}的伴隨數列{bn}的前50項之和；

（III）若數列{an}的前n項和（其中c為常數），求數列{an}的伴隨數列{bm}的前m項和Tm.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】在推導很多三角恒等變換公式時，我們可以利用平面向量的有關知識來研究，在一定程度上可以簡化推理過程.如我們就可以利用平面向量來推導兩角差的余弦公式:

具體過程如下：

如圖，在平面直角坐標系內作單位圓O，以為始邊作角.它們的終邊與單位圓O的交點分別為A，B.

則

由向量數量積的坐標表示，有：

設的夾角為θ，則

另一方面，由圖3.1—3（1）可知，；由圖可知，

.于是.

所以，也有，

所以，對于任意角有：（）

此公式給出了任意角的正弦、余弦值與其差角的余弦值之間的關系，稱為差角的余弦公式，簡記作.

有了公式以后，我們只要知道的值，就可以求得的值了.

閱讀以上材料，利用下圖單位圓及相關數據（圖中M是AB的中點），采取類似方法（用其他方法解答正確同等給分）解決下列問題：

（1）判斷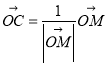是否正確？（不需要證明）

（2）證明：

（3）利用以上結論求函數的單調區間.

查看答案和解析>>

科目：高中數學 來源： 題型：

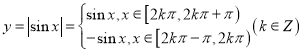【題目】（一）在函數圖象的學習中常常用到化歸轉化的思想，往往通過對一些已經學習過的函數圖象的研究，進一步遷移到其它函數，例如函數與正弦函數就有密切的聯系，因為.只需將在軸下方的圖象翻折到上方，就得到的圖象.

（二）在研究函數零點問題時，往往會將函數零點問題轉化為兩個函數圖象的交點問題.例如研究函數的零點就可以轉化為函數與函數的圖象交點來進行處理，通過作圖不僅知道函數有且僅有一個零點，還可以確定零點.這體現了化歸轉化與數形結合的思想在函數研究中的應用.

結合閱讀材料回答下面兩個問題：

作出函數的圖象；

利用作圖的方法驗證函數有且僅有兩個零點.若記兩個零點分別為，，證明：.（注：在同一坐標中作圖）

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】2019年，我國施行個人所得稅專項附加扣除辦法，涉及子女教育、繼續教育、大病醫療、住房貸款利息或者住房租金、贍養老人等六項專項附加扣除.某單位老、中、青員工分別有72，108，120人，現采用分層抽樣的方法，從該單位上述員工中抽取25人調查專項附加扣除的享受情況.

項目員工	A	B	C	D	E	F
子女教育	○	○	×	○	×	○
繼續教育	×	×	○	×	○	○
大病醫療	×	×	×	○	×	×
住房貸款利息	○	○	×	×	○	○
住房租金	×	×	○	×	×	×
贍養老人	○	○	×	×	×	○