
【題目】下表是某公司![]() 年
年![]() 月份研發費用
月份研發費用![]() (百萬元)和產品銷量
(百萬元)和產品銷量![]() (萬臺)的具體數據:
(萬臺)的具體數據:
月 份 |
|
|
|
|
|
|
|
|
研發費用(百萬元) |
|
|
|
|
|
|
|
|
產品銷量(萬臺) |
|
|
|
|
|
|
|
|
(1)根據數據可知![]() 與
與![]() 之間存在線性相關關系,用線性相關系數說明
之間存在線性相關關系,用線性相關系數說明![]() 與
與![]() 之間的相關性強弱程度
之間的相關性強弱程度
(2)求出![]() 與
與![]() 的線性回歸方程(系數精確到
的線性回歸方程(系數精確到![]() ),并估計當研發費用為
),并估計當研發費用為![]() (百萬元)時該產品的銷量.
(百萬元)時該產品的銷量.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]()
參照公式:相關系數 ,其回歸直線
,其回歸直線![]() 中的
中的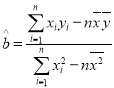
 同步輕松練習系列答案
同步輕松練習系列答案科目:高中數學 來源: 題型:
【題目】2019年,中國的國內生產總值(GDP)已經達到100億元人民幣,位居世界第二,這其中實體經濟的貢獻功不可沒,實體經濟組織一般按照市場化原則運行,某生產企業一種產品的成本由原料成本及非原料成本組成,每件產品的非原料成本![]() (元)與生產該產品的數量
(元)與生產該產品的數量![]() (千件)有關,經統計得到如下數據:
(千件)有關,經統計得到如下數據:

根據以上數據繪制了如下的散點圖
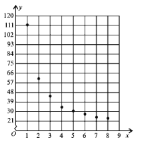
現考慮用反比例函數模型![]() 和指數函數模型
和指數函數模型![]() 分別對兩個變量關系進行擬合,為此變換如下:令
分別對兩個變量關系進行擬合,為此變換如下:令![]() ,則
,則![]() ,即
,即![]() 與
與![]() 也滿足線性關系,令
也滿足線性關系,令![]() ,則
,則![]() ,即
,即![]() 也滿足線線關系,這樣就可以使用最小二乘法求得非線性回歸方程,已求得用指數函數模型擬合的回歸方程為
也滿足線線關系,這樣就可以使用最小二乘法求得非線性回歸方程,已求得用指數函數模型擬合的回歸方程為![]() 與
與![]() 的相關系數
的相關系數![]() ,其他參考數據如下(其中
,其他參考數據如下(其中![]() )
)

(1)求指數函數模型和反比例函數模型中![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)試計算![]() 與
與![]() 的相關系數
的相關系數![]() ,并用相關系數判斷:選擇反比例函數和指數函數兩個模型中哪一個擬合效果更好(精確到0.01)?
,并用相關系數判斷:選擇反比例函數和指數函數兩個模型中哪一個擬合效果更好(精確到0.01)?
(3)根據(2)小題的選擇結果,該企業采用訂單生產模式(即根據訂單數量進行生產,產品全部售出),根據市場調研數據,該產品定價為100元時得到簽到訂單的情況如下表:
訂單數(千件) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
概率 |
|
|
|
|
|
|
|
|
|
|
|
已知每件產品的原來成本為10元,試估算企業的利潤是多少?(精確到1千元)
參考公式:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別是:
的斜率和截距的最小二乘估計分別是: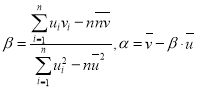 相關系數:
相關系數: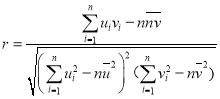
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代的數學名著,書中有如下問題:“今有五人分五錢,令上二人所得與下三人等.問各得幾何.”其意思為“已知甲、乙、丙、丁、戊五人分5錢,甲、乙兩人所得與丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差數列.問五人各得多少錢?”(“錢”是古代的一種重量單位).這個問題中,丙所得為( )
A.![]() 錢B.1錢C.
錢B.1錢C.![]() 錢D.
錢D.![]() 錢
錢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的離心率是
的離心率是![]() ,且以兩焦點間的線段為直徑的圓的內接正方形面積是
,且以兩焦點間的線段為直徑的圓的內接正方形面積是![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過左焦點![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() 、
、![]() 兩點,直線
兩點,直線![]() ,過
,過![]() 作垂直于
作垂直于![]() 的直線與直線
的直線與直線![]() 交于點
交于點![]() ,求
,求![]() 的最小值和此時的直線
的最小值和此時的直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 為橢圓
為橢圓![]() 的右焦點,且橢圓
的右焦點,且橢圓![]() 上的點到
上的點到![]() 的距離的最小值為
的距離的最小值為![]() ,過
,過![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,點
兩點,點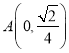 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)是否存在這樣的直線![]() ,使得以
,使得以![]() ,
,![]() 為鄰邊的平行四邊形為矩形?若存在,求出直線
為鄰邊的平行四邊形為矩形?若存在,求出直線![]() 的斜率;若不存在,請說明理由.
的斜率;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國剩余定理”又稱“孫子定理”,最早可見于中國南北朝時期的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”,原文如下:今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二.問物幾何?現有這樣一個相關的問題:將1到2020這2020個自然數中被5除余3且被7除余2的數按照從小到大的順序排成一列,構成一個數列,則該數列各項之和為( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為貫徹落實黨中央全面建設小康社會的戰略部署,某貧困地區的廣大黨員干部深入農村積極開展“精準扶貧”工作.經過多年的精心幫扶,截至2018年底,按照農村家庭人均年純收入8000元的小康標準,該地區僅剩部分家庭尚未實現小康.現從這些尚未實現小康的家庭中隨機抽取50戶,得到這50戶家庭2018年的家庭人均年純收入的頻率分布直方圖,如圖.
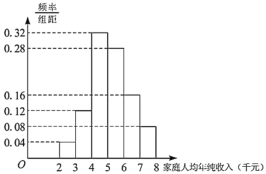
注:在頻率分布直方圖中,同一組數據用該區間的中點值作代表.
(1)估計該地區尚未實現小康的家庭2018年家庭人均年純收入的平均值;
(2)2019年7月,為估計該地能否在2020年全面實現小康,收集了當地最貧困的一戶家庭2019年1至6月的人均月純收入的數據,作出散點圖如下.
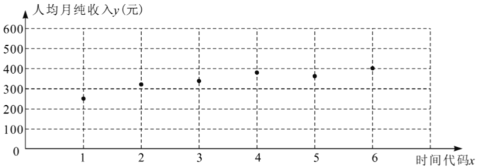
根據相關性分析,發現其家庭人均月純收入![]() 與時間代碼
與時間代碼![]() 之間具有較強的線性相關關系(記2019年1月、2月……分別為
之間具有較強的線性相關關系(記2019年1月、2月……分別為![]() ,
,![]() ,…,依此類推).試預測該家庭能否在2020年實現小康生活.
,…,依此類推).試預測該家庭能否在2020年實現小康生活.
參考數據:![]() ,
,![]() .
.
參考公式:線性回歸方程![]() 中,
中, ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com