
���}Ŀ����ֱ������(bi��o)ϵ![]() �У��c(di��n)
���c(di��n)![]() ��
��![]() ������
������![]() �ϵ�����һ�c(di��n)����(d��ng)�c(di��n)
�ϵ�����һ�c(di��n)����(d��ng)�c(di��n)![]() �M��
�M��![]()
��1�����c(di��n)![]() ��܉�E���̣�
��܉�E���̣�
��2����(j��ng)�^(gu��)�c(di��n)![]() �Ą�(d��ng)ֱ��
�Ą�(d��ng)ֱ��![]() �c�c(di��n)
�c�c(di��n)![]() ��܉�E���̽���
��܉�E���̽���![]() ���c(di��n)����
���c(di��n)����![]() �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)![]() �������c(di��n)
�������c(di��n)![]() ����ʹ��
����ʹ��![]() �������ڣ����
�������ڣ����![]() ������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
������(bi��o)���������ڣ�Ո(q��ng)�f(shu��)������.
���𰸡���1��![]() ����2�������c(di��n)
����2�������c(di��n)![]() �����}��.
�����}��.
��������
��1���O(sh��)![]() ��
��![]() ���������P(gu��n)�c(di��n)���뷨�õ��c(di��n)
���������P(gu��n)�c(di��n)���뷨�õ��c(di��n)![]() ��܉�E���̣�
��܉�E���̣�
��2���O(sh��)�����c(di��n)![]() ��ʹ��
��ʹ��![]() ���t
���t![]() ����?y��n)�ֱ��l�ăAб�Dz����ܞ�
����?y��n)�ֱ��l�ăAб�Dz����ܞ�![]() �����O(sh��)ֱ��l�ķ��̞�
�����O(sh��)ֱ��l�ķ��̞�![]() ������б�ʺ͞�0�����
������б�ʺ͞�0�����![]() ���Ķ��õ����c(di��n)����(bi��o).
���Ķ��õ����c(di��n)����(bi��o).
��1���O(sh��)![]() ��
��![]() ��
��
�t![]() ��
��![]() ��
��![]() .
.
��![]() ���t
���t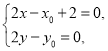 ��
��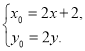
��?y��n)��c(di��n)N������![]() �ϵ�����һ�c(di��n)��
�ϵ�����һ�c(di��n)��
����![]() ��
��
����![]() ��������
��������![]() ��
��
���c(di��n)C��܉�E���̞�![]() .
.
��2���O(sh��)�����c(di��n)![]() ��ʹ��
��ʹ��![]() ������
������![]() .���}��֪��ֱ��l�ăAб�Dz����ܞ�
.���}��֪��ֱ��l�ăAб�Dz����ܞ�![]() �����O(sh��)ֱ��l�ķ��̞�
�����O(sh��)ֱ��l�ķ��̞�![]() ��
��
��![]() ����
����![]() ����
����![]() .�O(sh��)
.�O(sh��)![]() ��
��![]() ���t
���t![]() ��
��![]() .��?y��n)?/span>
.��?y��n)?/span>![]() ������
������![]() ����
����![]() ������
������![]() .�ʴ����c(di��n)
.�ʴ����c(di��n)![]() ��ʹ��
��ʹ��![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����![]() =(1,-3,2),
=(1,-3,2),![]() =(-2,1,1),�c(di��n)A(-3,-1,4),B(-2,-2,2).
=(-2,1,1),�c(di��n)A(-3,-1,4),B(-2,-2,2).
(1)��|2![]() +
+![]() |;
|;
(2)��ֱ��AB��,�Ƿ����һ�c(di��n)E,ʹ��![]() ��
�� ![]() ?(O��ԭ�c(di��n))
?(O��ԭ�c(di��n))
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������(sh��)![]() ij������֧�D���c����(bi��o)�S�քe׃���c(di��n)
ij������֧�D���c����(bi��o)�S�քe׃���c(di��n)![]() ���t����
���t����![]() ���н�ĺ͞飨 ��
���н�ĺ͞飨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��![]() ��
��![]() .
.
��1����![]() ��
��![]() ��������(sh��)����(sh��)��(sh��)a�ķ�����
��������(sh��)����(sh��)��(sh��)a�ķ�����
��2����![]() ��
��![]() ����Сֵ��3����(sh��)��(sh��)a��ֵ��
����Сֵ��3����(sh��)��(sh��)a��ֵ��
��3����![]() ��
��![]() �r(sh��)���������a��ȡֵ����.
�r(sh��)���������a��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���ڡ�ABC�У�a��b��c�քe���(n��i)��A��B��C�Č�(du��)߅����asin B����bsin![]() .
.
(1)��A��
(2)����ABC����eS��![]() c2����sin C��ֵ��
c2����sin C��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������(sh��)![]() ij������֧�D���c����(bi��o)�S�քe׃���c(di��n)
ij������֧�D���c����(bi��o)�S�քe׃���c(di��n)![]() ���t����
���t����![]() ���н�ĺ͞飨 ��
���н�ĺ͞飨 ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() .
.
(1)��(sh��)![]() �ĘOֵ�c(di��n)��(g��)��(sh��)��
�ĘOֵ�c(di��n)��(g��)��(sh��)��
(2)�� ���C��
���C��![]()
![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���W(xu��)Уˇ�g(sh��)��(ji��)��(du��)ͬһ�![]() ��
��![]() ��
��![]() ��
��![]() ���(xi��ng)��ِ��Ʒ��ֻ�u(p��ng)һ�(xi��ng)һ�Ȫ�(ji��ng)�����u(p��ng)��(ji��ng)�ҕ�ǰ���ס��ҡ���������λͬ�W(xu��)��(du��)�@���(xi��ng)��ِ��Ʒ�A(y��)�y(c��)���£�
���(xi��ng)��ِ��Ʒ��ֻ�u(p��ng)һ�(xi��ng)һ�Ȫ�(ji��ng)�����u(p��ng)��(ji��ng)�ҕ�ǰ���ס��ҡ���������λͬ�W(xu��)��(du��)�@���(xi��ng)��ِ��Ʒ�A(y��)�y(c��)���£�
���f(shu��)������![]() ��
��![]() ��Ʒ�@��һ�Ȫ�(ji��ng)����
��Ʒ�@��һ�Ȫ�(ji��ng)����
���f(shu��)����![]() ��Ʒ�@��һ�Ȫ�(ji��ng)����
��Ʒ�@��һ�Ȫ�(ji��ng)����
���f(shu��)����![]() ��
��![]() ���(xi��ng)��Ʒδ�@��һ�Ȫ�(ji��ng)����
���(xi��ng)��Ʒδ�@��һ�Ȫ�(ji��ng)����
���f(shu��)������![]() ��Ʒ�@��һ�Ȫ�(ji��ng)��.
��Ʒ�@��һ�Ȫ�(ji��ng)��.
���@��λͬ�W(xu��)��ֻ�Ѓ�λ�f(shu��)��Ԓ�nj�(du��)�ģ��t�@��һ�Ȫ�(ji��ng)����Ʒ��__________��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij���Ƅ�(d��ng)��˾������߷���(w��)�|(zh��)�����Q����(du��)ʹ��A��B�ɷN�ײ͵ļ��F(tu��n)�Ñ��M(j��n)���{(di��o)�飬��(zh��n)��ı���![]() ��(g��)�˔�(sh��)���^(gu��)1000�˵ĴF(tu��n)��8��(g��)�˔�(sh��)����200�˵�С���F(tu��n)���S�C(j��)��ȡ���ɂ�(g��)���F(tu��n)�M(j��n)���{(di��o)�飬��һ�γ�ȡ2��(g��)���F(tu��n)��ȫ��С���F(tu��n)�ĸ��ʞ�
��(g��)�˔�(sh��)���^(gu��)1000�˵ĴF(tu��n)��8��(g��)�˔�(sh��)����200�˵�С���F(tu��n)���S�C(j��)��ȡ���ɂ�(g��)���F(tu��n)�M(j��n)���{(di��o)�飬��һ�γ�ȡ2��(g��)���F(tu��n)��ȫ��С���F(tu��n)�ĸ��ʞ�![]() ��
��
![]() ��n��ֵ��
��n��ֵ��
![]() ��ȡ����2��(g��)���F(tu��n)��ͬһ��F(tu��n)����ȫ��F(tu��n)�ĸ��ʣ�
��ȡ����2��(g��)���F(tu��n)��ͬһ��F(tu��n)����ȫ��F(tu��n)�ĸ��ʣ�
![]() ��һ�γ�ȡ4��(g��)���F(tu��n)�����O(sh��)ȡ��С���F(tu��n)�Ă�(g��)��(sh��)��X����X�ķֲ��к�������
��һ�γ�ȡ4��(g��)���F(tu��n)�����O(sh��)ȡ��С���F(tu��n)�Ă�(g��)��(sh��)��X����X�ķֲ��к�������
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com