
【題目】已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,F1、F2分別是橢圓的左、右焦點,M為橢圓上除長軸端點外的任意一點,且△MF1F2的周長為4+2
,F1、F2分別是橢圓的左、右焦點,M為橢圓上除長軸端點外的任意一點,且△MF1F2的周長為4+2 ![]() .
.
(1)求橢圓C的方程;
(2)過點D(0,﹣2)作直線l與橢圓C交于A、B兩點,點N滿足 ![]() (O為原點),求四邊形OANB面積的最大值,并求此時直線l的方程.
(O為原點),求四邊形OANB面積的最大值,并求此時直線l的方程.
【答案】
(1)解:由離心率為e= ![]() =
= ![]() ,①
,①
則△MF1F2的周長l=2a+2c=4+2 ![]() ,則a+c=2+
,則a+c=2+ ![]() ,②
,②
則a=2,c= ![]() ,
,
則b2=a2﹣c2=1,
∴橢圓C的方程 ![]()
(2)解:由 ![]() ,則四邊形OANB為平行四邊形,
,則四邊形OANB為平行四邊形,
當直線l的斜率不存在時顯然不符合題意;
當直線l的斜率存在時,設直線l的方程為y=kx﹣2,l與橢圓交于A(x1,y1),B(x2,y2)兩點,由  得(1+4k2)x2﹣16kx+12=0
得(1+4k2)x2﹣16kx+12=0
由△=162k2﹣48(1+4k2)>0,得k2> ![]() ∴x1+x2=
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]()
∵S△OAB= ![]() 丨OD丨丨x1﹣x2丨=丨x1﹣x2丨,
丨OD丨丨x1﹣x2丨=丨x1﹣x2丨,
∴四邊形OANB面積S=2S△OAB=2丨x1﹣x2丨=2 ![]() ,
,
=2 ![]() ,
,
=2 ![]() ,
,
=8 ![]() ,
,
令4k2﹣3=t,則4k2=t+3(由上可知t>0),S=8 ![]() =8
=8 ![]() ≤8
≤8 ![]() =8
=8 ![]() =2,
=2,
當且僅當t=4,即k2= ![]() 時取等號;
時取等號;
∴當k=± ![]() ,平行四邊形OANB面積的最大值為2,
,平行四邊形OANB面積的最大值為2,
此時直線l的方程為y=± ![]() x﹣2
x﹣2
【解析】(1)利用橢圓的離心率公式及焦點三角形的周長公式,求得a和c的值,b2=a2﹣c2span>=1,即可求得橢圓方程;(2)確定四邊形OANB為平行四邊形,則SOANB=2S△OAB , 表示出面積,利用基本不等式,即可求得最大值,從而可得直線l的方程.
【考點精析】本題主要考查了橢圓的標準方程的相關知識點,需要掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() 才能正確解答此題.
才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】隨著國家二孩政策的全面放開,為了調查一線城市和非一線城市的二孩生育意愿,某機構用簡單隨機抽樣方法從不同地區調查了100位育齡婦女,結果如表.
非一線 | 一線 | 總計 | |
愿生 | 45 | 20 | 65 |
不愿生 | 13 | 22 | 35 |
總計 | 58 | 42 | 100 |
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
由K2= ![]() 算得,K2=
算得,K2= ![]() ≈9.616參照附表,得到的正確結論是( )
≈9.616參照附表,得到的正確結論是( )
A.在犯錯誤的概率不超過0.1%的前提下,認為“生育意愿與城市級別有關”
B.在犯錯誤的概率不超過0.1%的前提下,認為“生育意愿與城市級別無關”
C.有99%以上的把握認為“生育意愿與城市級別有關”
D.有99%以上的把握認為“生育意愿與城市級別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設雙曲線 ![]() (a>0,b>0)的左焦點為F1 , 左頂點為A,過F1作x軸的垂線交雙曲線于P、Q兩點,過P作PM垂直QA于M,過Q作QN垂直PA于N,設PM與QN的交點為B,若B到直線PQ的距離大于a+
(a>0,b>0)的左焦點為F1 , 左頂點為A,過F1作x軸的垂線交雙曲線于P、Q兩點,過P作PM垂直QA于M,過Q作QN垂直PA于N,設PM與QN的交點為B,若B到直線PQ的距離大于a+ ![]() ,則該雙曲線的離心率取值范圍是( )
,則該雙曲線的離心率取值范圍是( )
A.(1﹣ ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2 ![]() )
)
D.(2 ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是一個以A1B1C1為底面的直三棱柱被一平面所截得到的幾何體,截面為ABC,已知A1B1=B1C1=2,∠A1B1C1=90°,AA1=4,BB1=3,CC1=2,求:
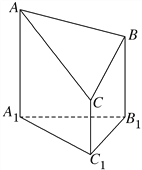
(Ⅰ)該幾何體的體積;
(Ⅱ)截面ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的右焦點為
的右焦點為![]() ,右頂點為
,右頂點為![]() ,已知
,已知![]() ,其中
,其中![]() 為原點,
為原點,![]() 為橢圓的離心率.
為橢圓的離心率.
(1)求橢圓的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓交于點
與橢圓交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,且
,且![]() ,求直線的
,求直線的![]() 斜率的取值范圍.
斜率的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(選修4﹣4:坐標系與參數方程)
已知曲線C1的參數方程為 ![]() (t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=2sinθ.
(t為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C2的極坐標方程為ρ=2sinθ.
(1)把C1的參數方程化為極坐標方程;
(2)求C1與C2交點的極坐標(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩地相距![]() ,汽車從甲地行駛到乙地,速度不得超過
,汽車從甲地行駛到乙地,速度不得超過![]() ,已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度
,已知汽車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度![]() (
(![]() )的平方成正比,比例系數為
)的平方成正比,比例系數為![]() ,固定部分為
,固定部分為![]() 元,
元,
(1)把全程運輸成本![]() (元)表示為速度
(元)表示為速度![]() (
(![]() )的函數,指出定義域;
)的函數,指出定義域;
(2)為了使全程運輸成本最小,汽車應以多大速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知x>0,由不等式x+ ![]() ≥2
≥2 ![]() =2,x+
=2,x+ ![]() =
= ![]() ≥3
≥3 ![]() =3,…,可以推出結論:x+
=3,…,可以推出結論:x+ ![]() ≥n+1(n∈N*),則a=( )
≥n+1(n∈N*),則a=( )
A.2n
B.3n
C.n2
D.nn
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com