
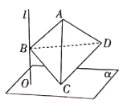
【題目】如圖,直線![]() 平面
平面![]() ,垂足為
,垂足為![]() ,三棱錐
,三棱錐![]() 的底面邊長和側(cè)棱長都為4,
的底面邊長和側(cè)棱長都為4,![]() 在平面
在平面![]() 內(nèi),
內(nèi),![]() 是直線
是直線![]() 上的動點,則點
上的動點,則點![]() 到平面
到平面![]() 的距離為_______,點
的距離為_______,點![]() 到直線
到直線![]() 的距離的最大值為_______.
的距離的最大值為_______.
【答案】![]()
![]()
【解析】
三棱錐![]() 的底面邊長和側(cè)棱長都為4,所以
的底面邊長和側(cè)棱長都為4,所以![]() 在平面
在平面![]() 的投影為
的投影為![]() 的重心,利用解直角三角形,即可求出點
的重心,利用解直角三角形,即可求出點![]() 到平面
到平面![]() 的距離;
的距離;![]() ,可得點
,可得點![]() 是以
是以![]() 為直徑的球面上的點,所以
為直徑的球面上的點,所以![]() 到直線
到直線![]() 的距離為以
的距離為以![]() 為直徑的球面上的點到
為直徑的球面上的點到![]() 的距離,
的距離,
最大距離為分別過![]() 和
和![]() 的兩個平行平面間距離加半徑,即可求出結(jié)論.
的兩個平行平面間距離加半徑,即可求出結(jié)論.
![]() 邊長為
邊長為![]() ,則中線長為
,則中線長為![]() ,
,
點![]() 到平面
到平面![]() 的距離為
的距離為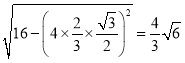 ,
,
點![]() 是以
是以![]() 為直徑的球面上的點,
為直徑的球面上的點,
所以![]() 到直線
到直線![]() 的距離為以
的距離為以![]() 為直徑的球面上的點到
為直徑的球面上的點到![]() 的距離,
的距離,
最大距離為分別過![]() 和
和![]() 的兩個平行平面間距離加半徑.
的兩個平行平面間距離加半徑.
又三棱錐![]() 的底面邊長和側(cè)棱長都為4,
的底面邊長和側(cè)棱長都為4,
以下求過![]() 和
和![]() 的兩個平行平面間距離,
的兩個平行平面間距離,
分別取![]() 中點
中點![]() ,連
,連![]() ,
,
則![]() ,同理
,同理![]() ,
,
分別過![]() 做
做![]() ,
,
直線![]() 確定平面
確定平面![]() ,直線
,直線![]() 確定平面
確定平面![]() ,
,
則![]() ,同理
,同理![]() ,
,
![]() 為所求,
為所求,![]() ,
,
![]() ,
,
所以![]() 到直線
到直線![]() 最大距離為
最大距離為![]() .
.
故答案為:![]() ;
;![]() .
.


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:高中數(shù)學 來源: 題型:
【題目】在開展學習強國的活動中,某校高三數(shù)學教師成立了黨員和非黨員兩個學習組,其中黨員學習組有4名男教師、1名女教師,非黨員學習組有2名男教師、2名女教師,高三數(shù)學組計劃從兩個學習組中隨機各選2名教師參加學校的挑戰(zhàn)答題比賽.
(1)求選出的4名選手中恰好有一名女教師的選派方法數(shù);
(2)記X為選出的4名選手中女教師的人數(shù),求X的概率分布和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知在![]() 中,兩直角邊
中,兩直角邊![]() ,
,![]() 的長分別為
的長分別為![]() 和
和![]() ,以
,以![]() 的中點
的中點![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,以
軸,以![]() 的垂直平分線為
的垂直平分線為![]() 軸建立平面直角坐標系,橢圓
軸建立平面直角坐標系,橢圓![]() 以
以![]() ,
,![]() 為焦點,且經(jīng)過點
為焦點,且經(jīng)過點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() :
:![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,在
兩點,在![]() 軸上是否存在點
軸上是否存在點![]() ,使得
,使得![]() 為等邊三角形,若存在,求出直線
為等邊三角形,若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知動圓過定點![]() ,且與直線
,且與直線![]() 相切,動圓圓心的軌跡為
相切,動圓圓心的軌跡為![]() ,過
,過![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與
與![]() 交于兩點
交于兩點![]() ,過
,過![]() 分別作
分別作![]() 的切線,兩切線的交點為
的切線,兩切線的交點為![]() ,直線
,直線![]() 與
與![]() 交于兩點
交于兩點![]() .
.
(1)證明:點![]() 始終在直線
始終在直線![]() 上且
上且![]() ;
;
(2)求四邊形![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓![]() ,定點
,定點![]() ,
,![]() 為平面內(nèi)一動點,以線段
為平面內(nèi)一動點,以線段![]() 為直徑的圓內(nèi)切于圓
為直徑的圓內(nèi)切于圓![]() ,設動點
,設動點![]() 的軌跡為曲線
的軌跡為曲線![]()
(1)求曲線![]() 的方程
的方程
(2)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,已知點
兩點,已知點![]() ,直線
,直線![]() 分別與直線
分別與直線![]() 交于
交于![]() 兩點,線段
兩點,線段![]() 的中點
的中點![]() 是否在定直線上,若存在,求出該直線方程;若不是,說明理由.
是否在定直線上,若存在,求出該直線方程;若不是,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“一帶一路”是“絲綢之路經(jīng)濟帶”和“21世紀海上絲綢之路”的簡稱,旨在積極發(fā)展我國與沿線國家經(jīng)濟合作關(guān)系,共同打造政治互信、經(jīng)濟融合、文化包容的命運共同體.自2015年以來,“一帶一路”建設成果顯著.如圖是2015—2019年,我國對“一帶一路”沿線國家進出口情況統(tǒng)計圖,下列描述錯誤的是( )
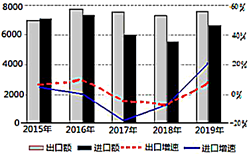
A.這五年,出口總額之和比進口總額之和大
B.這五年,2015年出口額最少
C.這五年,2019年進口增速最快
D.這五年,出口增速前四年逐年下降
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
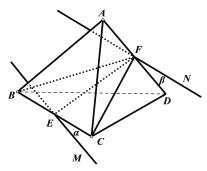
【題目】如圖,在三棱錐![]() 中,
中, ![]() 底面
底面![]() 分別是
分別是![]() 的中點,
的中點, ![]() 在
在![]() ,且
,且![]() .
.
(1)求證: ![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;
的長;
若不存在,請說明理由.

查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com