
【題目】已知![]() (
(![]() 且
且![]() )在區間
)在區間![]() 上的最大值與最小值之和為
上的最大值與最小值之和為![]() ,
,![]() ,其中
,其中![]() .
.
(1)直接寫出![]() 的解析式和單調性;
的解析式和單調性;
(2)若![]() 對
對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若
,若![]() ,使得對
,使得對![]() ,都有
,都有![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ,減函數;(2)
,減函數;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)分![]() 和
和![]() 兩種情況討論函數
兩種情況討論函數![]() 在區間
在區間![]() 上單調性,得出
上單調性,得出![]() ,可解出實數
,可解出實數![]() 的值,并判斷出函數
的值,并判斷出函數![]() 的單調性;
的單調性;
(2)由![]() ,可得出
,可得出![]() 對任意的實數
對任意的實數![]() 恒成立,由參變量分離法得出
恒成立,由參變量分離法得出![]() ,求出
,求出![]() 的取值范圍,即可得出實數
的取值范圍,即可得出實數![]() 的取值范圍;
的取值范圍;
(3)由題意可得![]() ,求出函數
,求出函數![]() 在區間
在區間![]() 上的最大值,然后分
上的最大值,然后分![]() 與
與![]() 的大小關系,求出函數
的大小關系,求出函數![]() 在區間
在區間![]() 上最大值
上最大值![]() ,然后解出不等式
,然后解出不等式![]() 即可得出實數
即可得出實數![]() 的取值范圍.
的取值范圍.
(1)當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上為增函數;
上為增函數;
當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上為減函數.
上為減函數.
由題意可得![]() ,即
,即![]() ,
,
![]() 且
且![]() ,解得
,解得![]() ,
,![]() ,則函數
,則函數![]() 為減函數;
為減函數;
(2)由(1)可得![]() ,由
,由![]() ,即
,即![]() ,即
,即![]() ,即
,即![]() 對任意的
對任意的![]() 恒成立,即
恒成立,即![]() .
.
![]() ,
,![]() ,
,![]() ,因此,實數
,因此,實數![]() 的取值范圍是
的取值范圍是![]() ;
;
(3)![]() 函數
函數![]() 在區間
在區間![]() 上單調遞減,則
上單調遞減,則![]() .
.
由題意可得,![]() .
.
二次函數![]() 的圖象開口向上,對稱軸為直線
的圖象開口向上,對稱軸為直線![]() .
.
當![]() 時,且當
時,且當![]() 時,
時,![]() ,則
,則![]() ,解得
,解得![]() ,此時
,此時![]() ;
;
當![]() 時,且當
時,且當![]() 時,
時,![]() ,則
,則![]() ,解得
,解得![]() ,此時
,此時![]() .
.
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案科目:高中數學 來源: 題型:
【題目】某市2013年發放汽車牌照12萬張,其中燃油型汽車牌照10萬張,電動型汽車2萬張,為了節能減排和控制總量,從2013年開始,每年電動型汽車牌照按50%增長,而燃油型汽車牌照每一年比上一年減少0.5萬張,同時規定一旦某年發放的牌照超過15萬張,以后每一年發放的電動車的牌照的數量維持在這一年的水平不變.
(1)記2013年為第一年,每年發放的燃油型汽車牌照數量構成數列![]() ,每年發放電動型汽車牌照數為構成數列
,每年發放電動型汽車牌照數為構成數列![]() ,完成下列表格,并寫出這兩個數列的通項公式;
,完成下列表格,并寫出這兩個數列的通項公式;
(2)從2013年算起,累計各年發放的牌照數,哪一年開始超過200萬張?
|
|
|
| |
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓C:![]() 的離心率為
的離心率為![]() ,并且橢圓經過點P(1,
,并且橢圓經過點P(1,![]() ),直線l的方程為x=4.
),直線l的方程為x=4.
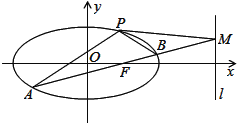
(1)求橢圓的方程;
(2)已知橢圓內一點E(1,0),過點E作一條斜率為k的直線與橢圓交于A,B兩點,交直線l于點M,記PA,PB,PM的斜率分別為k1,k2,k3.問:是否存在常數![]() ,使得k1+k2=
,使得k1+k2=![]() k3?若存在,求出
k3?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
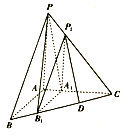
【題目】如圖,在三棱錐![]() 中,
中,![]() 兩兩垂直,
兩兩垂直,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 與棱
與棱![]() 分別交于
分別交于![]() 三點.
三點.
(1)過![]() 作直線
作直線![]() ,使得
,使得![]() ,
,![]() ,請寫出作法并加以證明;
,請寫出作法并加以證明;
(2)若α將三梭錐P﹣ABC分成體積之比為8:19的兩部分(其中,四面體P1A1B1C的體積更小),D為線段B1tC的中點,求直線P1D與平面PA1B1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中點點P在線段A1B上.
2,AB⊥AC,M是棱BC的中點點P在線段A1B上.
(1)若P是線段A1B的中點,求直線MP與直線AC所成角的大小;
(2)若![]() 是
是![]() 的中點,直線
的中點,直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求線段BP的長度.
,求線段BP的長度.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代名詞“芻童”原來是草堆的意思,關于“芻童”體積計算的描述,《九章算術》注曰:“倍上袤,下袤從之,亦倍下袤,上袤從之,各以其廣乘之,并,以高乘之,皆六而一.”其計算方法是:將上底面的長乘二,與下底面的長相加,再與上底面的寬相乘,將下底面的長乘二,與上底面的長相加,再與下底面的寬相乘;把這兩個數值相加,與高相乘,再取其六分之一.已知一個“芻童”的下底面是周長為18的矩形,上底面矩形的長為3,寬為2,“芻童”的高為3,則該“芻童”的體積的最大值為
A. ![]() B.
B. ![]() C. 39 D.
C. 39 D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數 ,下列判斷正確的是( )
,下列判斷正確的是( )
A. ![]() 有最大值和最小值
有最大值和最小值
B. ![]() 的圖象的對稱中心為
的圖象的對稱中心為![]() (
(![]() )
)
C. ![]() 在
在![]() 上存在單調遞減區間
上存在單調遞減區間
D. ![]() 的圖象可由
的圖象可由![]() 的圖象向左平移
的圖象向左平移![]() 個單位而得
個單位而得
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】空氣質量指數(Air Quality Index,簡稱AQI)是定量描述空氣質量狀況的質量指數.空氣質量按照AQI大小分為六級:0~50為優;51~100為良;101~150為輕度污染;151~200為中度污染;201~300為重度污染;大于300為嚴重污染.一環保人士記錄去年某地某月10天的AQI的莖葉圖如圖.利用該樣本估計該地本月空氣質量優良(![]() )的天數(按這個月總共30天計算)為________.
)的天數(按這個月總共30天計算)為________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 的圖象在
的圖象在![]() 處的切線經過點
處的切線經過點![]() ,求
,求![]() 的值;
的值;
(2)是否存在負整數![]() ,使函數
,使函數![]() 的極大值為正值?若存在,求出所有負整數
的極大值為正值?若存在,求出所有負整數![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com