
【題目】為方便市民出行,倡導低碳出行.某市公交公司推出利用支付寶和微信掃碼支付乘車活動,活動設置了一段時間的推廣期,在推廣期內采用隨機優惠鼓勵市民掃碼支付乘車.該公司某線路公交車隊統計了活動推廣期第一周內使用掃碼支付的情況,其中![]() (單位:天)表示活動推出的天次,
(單位:天)表示活動推出的天次,![]() (單位:十人次)表示當天使用掃碼支付的人次,整理后得到如圖所示的統計表1和散點圖.
(單位:十人次)表示當天使用掃碼支付的人次,整理后得到如圖所示的統計表1和散點圖.
表1:
x | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 | 第6天 | 第7天 |
y | 7 | 12 | 20 | 33 | 54 | 90 | 148 |

(1)由散點圖分析后,可用![]() 作為該線路公交車在活動推廣期使用掃碼支付的人次
作為該線路公交車在活動推廣期使用掃碼支付的人次![]() 關于活動推出天次
關于活動推出天次![]() 的回歸方程,根據表2的數據,求此回歸方程,并預報第8天使用掃碼支付的人次(精確到整數).
的回歸方程,根據表2的數據,求此回歸方程,并預報第8天使用掃碼支付的人次(精確到整數).
表2:
|
|
| img src="http://thumb.zyjl.cn/questionBank/Upload/2019/08/08/08/88254471/SYS201908080801220877999013_ST/SYS201908080801220877999013_ST.008.png" width="67" height="40" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" /> |
|
|
4 | 52 | 3.5 | 140 | 2069 | 112 |
表中![]() ,
,![]() .
.
(2)推廣期結束后,該車隊對此期間乘客的支付情況進行統計,結果如表3.
表3:
支付方式 | 現金 | 乘車卡 | 掃碼 |
頻率 | 10% | 60% | 30% |
優惠方式 | 無優惠 | 按7折支付 | 隨機優惠(見下面統計結果) |
統計結果顯示,掃碼支付中享受5折支付的頻率為![]() ,享受7折支付的頻率為
,享受7折支付的頻率為![]() ,享受9折支付的頻率為
,享受9折支付的頻率為![]() .已知該線路公交車票價為1元,將上述頻率作為相應事件發生的概率,記隨機變量
.已知該線路公交車票價為1元,將上述頻率作為相應事件發生的概率,記隨機變量![]() 為在活動期間該線路公交車搭載乘客一次的收入(單位:元),求
為在活動期間該線路公交車搭載乘客一次的收入(單位:元),求![]() 的分布列和期望.
的分布列和期望.
參考公式:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為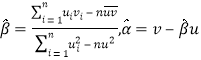 參考數據:
參考數據:![]() ,
,![]() ,
,![]() .
.
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:①“![]() ”是“
”是“![]() ”成立的必要不充分條件②命題“若
”成立的必要不充分條件②命題“若![]() ,則
,則![]() ”的否命題是:“若
”的否命題是:“若![]() ,則
,則![]() ”;③命題“
”;③命題“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,均有
,均有![]() ”④如果命題“
”④如果命題“![]() ”與命題“
”與命題“![]() ”都是真命題,那么命題
”都是真命題,那么命題![]() 一定是真命題;其中為真命題的個數是( )
一定是真命題;其中為真命題的個數是( )
A.4個B.3個C.2個D.1個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A,B分別是雙曲線![]() 的左右頂點,設過
的左右頂點,設過![]() 的直線PA,PB與雙曲線分別交于點M,N,直線MN交x軸于點Q,過Q的直線交雙曲線的于S,T兩點,且
的直線PA,PB與雙曲線分別交于點M,N,直線MN交x軸于點Q,過Q的直線交雙曲線的于S,T兩點,且![]() ,則
,則![]() 的面積( )
的面積( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C經過A(5,3),B(4,4)兩點,且圓心在x軸上.
(1)求圓C的標準方程;
(2)若直線l過點(5,2),且被圓C所截得的弦長為6,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知極坐標系的極點在平面直角坐標系的原點![]() 處,極軸與
處,極軸與![]() 軸的非負半軸重合,且長度單位相同,直線
軸的非負半軸重合,且長度單位相同,直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() (
(![]() 為參數).其中
為參數).其中![]() .
.
(1)試寫出直線![]() 的直角坐標方程及曲線
的直角坐標方程及曲線![]() 的普通方程;
的普通方程;
(2)若點![]() 為曲線
為曲線![]() 上的動點,求點
上的動點,求點![]() 到直線
到直線![]() 距離的最大值.
距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() ,以原點0為極點,
,以原點0為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若曲線![]() 方程中的參數是
方程中的參數是![]() ,且
,且![]() 與
與![]() 有且只有一個公共點,求
有且只有一個公共點,求![]() 的普通方程;
的普通方程;
(2)已知點![]() ,若曲線
,若曲線![]() 方程中的參數是
方程中的參數是![]() ,
,![]() ,且
,且![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩個不同點,求
兩個不同點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖1是由菱形![]() ,平行四邊形
,平行四邊形![]() 和矩形
和矩形![]() 組成的一個平面圖形,其中
組成的一個平面圖形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,將其沿
,將其沿![]() ,
,![]() 折起使得
折起使得![]() 與
與![]() 重合,如圖2.
重合,如圖2.

(1)證明:圖2中的平面![]() 平面
平面![]() ;
;
(2)求圖2中點![]() 到平面
到平面![]() 的距離;
的距離;
(3)求圖2中二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學典籍《九章算術》第七章“盈不足”中有一問題:“今有蒲生一日,長三尺,莞生一日,長一尺.蒲生日自半.莞生日自倍.問幾何日而長等?”(蒲常指一種多年生草本植物,莞指水蔥一類的植物)現欲知幾日后,莞高超過蒲高一倍.為了解決這個新問題,設計如圖所示的程序框圖,輸入![]() ,
,![]() .那么在①處應填_______和輸出
.那么在①處應填_______和輸出![]() 的值為( )
的值為( )
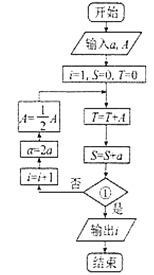
A. ![]() 4B.
4B. ![]() 4
4
C. ![]() 3D.
3D. ![]() 3
3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com