
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 的方程為
的方程為![]() ,過點
,過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于兩點
交于兩點![]() ,
,![]() .
.
(1)若![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)若直線![]() 與
與![]() 軸交于點
軸交于點![]() ,設
,設![]() ,
,![]() ,
,![]() ,
,![]() R,求
R,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)設斜率為![]() ,則直線
,則直線![]() 的方程為
的方程為![]() ,利用圓的弦長公式,列出方程求得
,利用圓的弦長公式,列出方程求得![]() 的值,即可得到直線的方程;
的值,即可得到直線的方程;
(2)當直線![]() 的斜率不存在時,根據向量的運算,求得
的斜率不存在時,根據向量的運算,求得![]() ,當直線
,當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 的方程為
的方程為![]() ,聯立方程組,利用根與系數的關系,以及向量的運算,求得
,聯立方程組,利用根與系數的關系,以及向量的運算,求得![]() ,得到答案.
,得到答案.
(1)當直線![]() 的斜率不存在時,
的斜率不存在時,![]() ,不符合題意;
,不符合題意;
當直線![]() 的斜率存在時,設斜率為
的斜率存在時,設斜率為![]() ,則直線
,則直線![]() 的方程為
的方程為![]() ,
,
所以圓心![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
因為![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以直線![]() 的方程為
的方程為![]() . .
. .
(2)當直線![]() 的斜率不存在時,不妨設
的斜率不存在時,不妨設![]() ,
,![]() ,
,![]() ,
,
因為![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() .
.
當直線![]() 的斜率存在時,設斜率為
的斜率存在時,設斜率為![]() ,則直線
,則直線![]() 的方程為:
的方程為:![]() ,
,
因為直線![]() 與
與![]() 軸交于點
軸交于點![]() ,所以
,所以![]() .
.
直線![]() 與圓
與圓![]() 交于點
交于點![]() ,
,![]() ,設
,設![]() ,
,![]() ,
,
由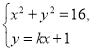 得,
得,![]() ,所以
,所以![]() ,
,![]() ;
;
因為![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以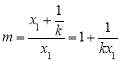 ,
,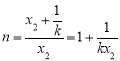 ,
,
所以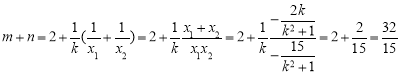 .
.
綜上,![]() .
.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:高中數學 來源: 題型:
【題目】設函數 f(x)=|x+2|﹣|x﹣3|﹣a
(Ⅰ)當 a=1 時,求函數 f(x)的最大值;
(Ⅱ)若 f(x)≤ ![]() 對任意 x∈R 恒成立,求實數 a 的取值范圍.
對任意 x∈R 恒成立,求實數 a 的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】李克強總理在2018年政府工作報告指出,要加快建設創新型國家,把握世界新一輪科技革命和產業變革大勢,深入實施創新驅動發展戰略,不斷增強經濟創新力和競爭力.某手機生產企業積極響應政府號召,大力研發新產品,爭創世界名牌.為了對研發的一批最新款手機進行合理定價,將該款手機按事先擬定的價格進行試銷,得到一組銷售數據![]() ,如表所示:
,如表所示:
單價 |
|
|
|
|
|
|
銷量 |
|
|
|
|
|
|
已知![]() .
.
(1)若變量![]() 具有線性相關關系,求產品銷量
具有線性相關關系,求產品銷量![]() (百件)關于試銷單價
(百件)關于試銷單價![]() (千元)的線性回歸方程
(千元)的線性回歸方程![]() ;
;
(2)用(1)中所求的線性回歸方程得到與![]() 對應的產品銷量的估計值
對應的產品銷量的估計值![]() .
.
(參考公式:線性回歸方程中![]() 的估計值分別為
的估計值分別為 )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三條直線型公路![]() ,
,![]() ,
,![]() 在點
在點![]() 處交匯,其中
處交匯,其中![]() 與
與![]() 、
、![]() 與
與![]() 的夾角都為
的夾角都為![]() ,在公路
,在公路![]() 上取一點
上取一點![]() ,且
,且![]() km,過
km,過![]() 鋪設一直線型的管道
鋪設一直線型的管道![]() ,其中點
,其中點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上(
上(![]() ,
,![]() 足夠長),設
足夠長),設![]() km,
km,![]() km.
km.
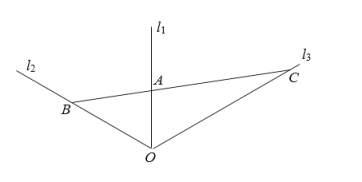
(1)求出![]() ,
,![]() 的關系式;
的關系式;
(2)試確定![]() ,
,![]() 的位置,使得公路
的位置,使得公路![]() 段與
段與![]() 段的長度之和最小.
段的長度之和最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區有小學21所,中學14所,現采用分層抽樣的方法從這些學校中抽取5所學校,對學生進行視力檢查.
(1)求應從小學、中學中分別抽取的學校數目;
(2)若從抽取的5所學校中抽取2所學校作進一步數據
①列出所有可能抽取的結果;
②求抽取的2所學校至少有一所中學的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有人用三段論進行推理:“函數![]() 的導函數
的導函數![]() 的零點即為函數
的零點即為函數![]() 的極值點,函數
的極值點,函數![]() 的導函數的零點為
的導函數的零點為![]() ,所以
,所以![]() 是函數
是函數![]() 的極值點 ”,上面的推理錯誤的是( )
的極值點 ”,上面的推理錯誤的是( )
A. 大前提 B. 小前提 C. 推理形式 D. 以上都是
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】正方體ABCD﹣A1B1C1D1的棱長為1,點E,F分別是棱D1C1 , B1C1的中點,過E,F作一平面α,使得平面α∥平面AB1D1 , 則平面α截正方體的表面所得平面圖形為( )
A.三角形
B.四邊形
C.五邊形
D.六邊形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com