
【題目】設![]() 、
、![]() 為雙曲線
為雙曲線![]() 上的兩點,
上的兩點,![]() 為線段
為線段![]() 的中點,線段
的中點,線段![]() 的垂直平分線與雙曲線交于
的垂直平分線與雙曲線交于![]() 、
、![]() 兩點
兩點
(1)確定![]() 的取值范圍
的取值范圍
(2)試判斷![]() 、
、![]() 、
、![]() 、
、![]() 四點是否共圓?并說明理由
四點是否共圓?并說明理由
 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,長方體![]() 的長,寬,高分別為4,3,5,現有一甲殼蟲從
的長,寬,高分別為4,3,5,現有一甲殼蟲從![]() 點出發沿長方體表面爬行到
點出發沿長方體表面爬行到![]() 點來獲取食物.
點來獲取食物.
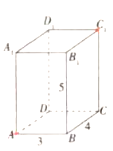
(1)甲殼蟲想盡快獲取食物可通過哪些路徑獲取?
(2)哪條獲取食物的路徑最短?最短為多少?
(3)此類問題的一般處理方法是什么?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中央政府為了應對因人口老齡化而造成的勞動力短缺等問題,擬定出臺“延遲退休年齡政策”.為了解人們對“延遲退休年齡政策”的態度,責成人社部進行調研.人社部從網上年齡在15~65歲的人群中隨機調查100人,調查數據的頻率分布直方圖和支持“延遲退休”的人數與年齡的統計結果如下:


(1)由以上統計數據填![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異;
列聯表,并判斷能否在犯錯誤的概率不超過0.05的前提下認為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異;

(2)若以45歲為分界點,從不支持“延遲退休”的人中按分層抽樣的方法抽取8人參加某項活動.現從這8人中隨機抽2人.
①抽到1人是45歲以下時,求抽到的另一人是45歲以上的概率.
②記抽到45歲以上的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
參考數據:
![]()
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱![]() (底面為正三角形,側棱和底面垂直)的所有棱長都為2,
(底面為正三角形,側棱和底面垂直)的所有棱長都為2,![]() 為
為![]() 的中點,O為
的中點,O為![]() 中點.
中點.
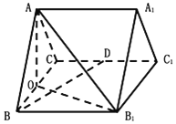
(1)求證:![]() 平面
平面![]() .
.
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了迎接旅游旺季的到來,少林寺設置了一個專門安排旅客住宿的客棧,寺廟的工作人員發現為游客準備的食物有些月份剩余不少,浪費很嚴重,為了控制經營成本,減少浪費,就想適時調整投入.為此他們統計每個月入住的游客人數,發現每年各個月份來客棧入住的游客人數會呈現周期性的變化,并且有以下規律:
①每年相同的月份,入住客棧的游客人數基本相同;
②入住客棧的游客人數在![]() 月份最少,在
月份最少,在![]() 月份最多,相差約
月份最多,相差約![]() 人;
人;
③![]() 月份入住客棧的游客約為
月份入住客棧的游客約為![]() 人,隨后逐月增加直到
人,隨后逐月增加直到![]() 月份達到最多.
月份達到最多.
(1)試用一個正弦型三角函數描述一年中入住客棧的游客人數與月份之間的關系;
(2)請問哪幾個月份要準備![]() 份以上的食物?
份以上的食物?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于函數![]() ,總存在實數
,總存在實數![]() ,使
,使![]() 成立,則稱
成立,則稱![]() 為
為![]() 關于參數
關于參數![]() 的不動點.
的不動點.
(1)當![]() ,
,![]() 時,求
時,求![]() 關于參數
關于參數![]() 的不動點;
的不動點;
(2)若對任意實數![]() ,函數
,函數![]() 恒有關于參數
恒有關于參數![]() 兩個不動點,求
兩個不動點,求![]() 的取值范圍;
的取值范圍;
(3)當![]() ,
,![]() 時,函數
時,函數![]() 在
在![]() 上存在兩個關于參數
上存在兩個關于參數![]() 的不動點,試求參數
的不動點,試求參數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司欲生產一款迎春工藝品回饋消費者,工藝品的平面設計如圖所示,該工藝品由直角![]() 和以
和以![]() 為直徑的半圓拼接而成,點
為直徑的半圓拼接而成,點![]() 為半圈上一點(異于
為半圈上一點(異于![]() ,
,![]() ),點
),點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() .已知
.已知![]() ,
,![]() ,設
,設![]() .
.

(1)為了使工藝禮品達到最佳觀賞效果,需滿足![]() ,且
,且![]() 達到最大.當
達到最大.當![]() 為何值時,工藝禮品達到最佳觀賞效果;
為何值時,工藝禮品達到最佳觀賞效果;
(2)為了工藝禮品達到最佳穩定性便于收藏,需滿足![]() ,且
,且![]() 達到最大.當
達到最大.當![]() 為何值時,
為何值時,![]() 取得最大值,并求該最大值.
取得最大值,并求該最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究性學習小組對春季晝夜溫差大小與某花卉種子發芽多少之間的關系進行研究,他們分別記錄了3月1日至3月5日的每天晝夜溫差與實驗室每天每100顆種子浸泡后的發芽數,得到如下資料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
溫差 | 10 | 11 | 13 | 12 | 9 |
發芽數 | 23 | 25 | 30 | 26 | 16 |
(1)從3月1日至3月5日中任選2天,記發芽的種子數分別為![]() ,
,![]() ,求事件“
,求事件“![]() ”的概率;
”的概率;
(2)該小組發現種子的發芽數![]() (顆)與晝夜溫差
(顆)與晝夜溫差![]() (℃)呈線性相關關系,試求:線性回歸方程
(℃)呈線性相關關系,試求:線性回歸方程![]() .
.
(參考公式:線性回歸方程![]() 中系數計算公式
中系數計算公式 ,
,![]() .其中
.其中![]() ,
,![]() 表示樣本均值.
表示樣本均值.
參考數據:![]() ;
;![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com