【題目】已知拋物線
：
經過點
，直線
分別與拋物線交于點
，若直線的斜率之和為零，則直線
的斜率為_________。
【答案】-2
【解析】
將P（1，4）代入y2＝2px可解得p＝8，得拋物線方程為y2＝16x，在設出直線PA的方程并與拋物線方程聯立解得A的坐標，同理解得B的坐標，最后用斜率公式可求得AB的斜率為定值﹣2．
因為拋物線C：y2＝2px經過點P（1，4），∴p＝8，∴拋物線C：y2＝16x，設直線PA：y﹣4＝k（x﹣1），并代入y2＝16x消去x并整理得k2x2+（8k﹣2k2﹣16）xx+（4﹣k）2＝0，
設A（x1，y1），B（x2，y2）依題意知1和x1是以上一元二次方程的兩個根，∴1x1＝
，∴x1＝
，∴y1＝4﹣k+kx1＝4﹣k+k＝
﹣4，同理得x2＝
，y2＝﹣﹣4，所以直線AB的斜率為：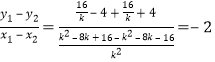
．
故答案為：﹣2
一本好題口算題卡系列答案科目：高中數學 來源： 題型：
【題目】一場小型晚會有
個唱歌節目和
個相聲節目，要求排出一個節目單．
（1）個相聲節目要排在一起，有多少種排法？
（2）個相聲節目彼此要隔開，有多少種排法？
（3）第一個節目和最后一個節目都是唱歌節目，有多少種排法？
（4）前個節目中要有相聲節目，有多少種排法？
（要求：每小題都要有過程，且計算結果都用數字表示）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著國家二孩政策的全面放開，為了調查一線城市和非一線城市的二孩生育意愿，某機構用簡單隨機抽樣方法從不同地區調查了
位育齡婦女，結果如表.
非一線 | 一線 | 總計 | |
愿生 |
|
|
|
不愿生 |
|
|
|
總計 |
|
|
|
附表：
|
|
|
|
|
|
|
|
由
算得，
參照附表，得到的正確結論是（ ）
A. 在犯錯誤的概率不超過
的前提下，認為“生育意愿與城市級別有關”
B. 有
以上的把握認為“生育意愿與城市級別有關”
C. 在犯錯誤的概率不超過的前提下，認為“生育意愿與城市級別無關”
D. 有以上的把握認為“生育意愿與城市級別無關”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的左、右焦點分別為
，
是橢圓上的點，且
的面積為
。
（1）求橢圓的方程；
（2）若斜率為
且在
軸上的截距為
的直線
與橢圓相交于兩點
，若橢圓上存在點
，滿足
，其中
是坐標原點，求的值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2018年“雙十一”期間，某商場舉辦了一次有獎促銷活動，顧客消費每滿1000元可參加一次抽獎(例如：顧客甲消費930元，不得參與抽獎；顧客乙消費3400元，可以抽獎三次)。如圖1，在圓盤上繪制了標有A，B，C，D的八個扇形區域，每次抽獎時由顧客按動按鈕使指針旋轉一次，旋轉結束時指針會隨機停在圓盤上的某一個位置，顧客獲獎的獎次由指針所指區域決定(指針與區域邊界線粗細忽略不計)。商家規定：指針停在標A，B，C，D的扇形區域分別對應的獎金為200元、150元、100元和50元。已知標有A，B，C，D的扇形區域的圓心角成等差數列，且標D的扇形區域的圓心角是標A的扇形區域的圓心角的4倍．
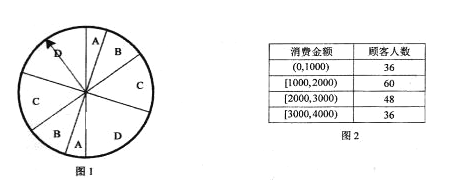
(I)某顧客只抽獎一次，設該顧客抽獎所獲得的獎金數為X元，求X的分布列和數學期望；
(II)如圖2，該商場統計了活動期間一天的顧客消費情況．現按照消費金額分層抽樣選出15位顧客代表，其中獲得獎金總數不足100元的顧客代表有7位．現從這7位顧客代表中隨機選取兩位，求這兩位顧客的獎金總數和仍不足100元的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】改革開放以來，人們的支付方式發生了巨大轉變．近年來，移動支付已成為主要支付方式之一．為了解某校學生上個月A，B兩種移動支付方式的使用情況，從全校所有的1000名學生中隨機抽取了100人，發現樣本中A，B兩種支付方式都不使用的有5人，樣本中僅使用A和僅使用B的學生的支付金額分布情況如下：
支付方式 | 不大于2000元 | 大于2000元 |
僅使用A | 27人 | 3人 |
僅使用B | 24人 | 1人 |
（Ⅰ）估計該校學生中上個月A，B兩種支付方式都使用的人數；
（Ⅱ）從樣本僅使用B的學生中隨機抽取1人，求該學生上個月支付金額大于2000元的概率；
（Ⅲ）已知上個月樣本學生的支付方式在本月沒有變化．現從樣本僅使用B的學生中隨機抽查1人，發現他本月的支付金額大于2000元．結合（Ⅱ）的結果，能否認為樣本僅使用B的學生中本月支付金額大于2000元的人數有變化？說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，某公園內有兩條道路
，
，現計劃在上選擇一點
，新建道路
，并把
所在的區域改造成綠化區域．已知
，
．
（1）若綠化區域的面積為1
，求道路的長度；
（2）若綠化區域改造成本為10萬元/，新建道路成本為10萬元/．設
（
），當
為何值時，該計劃所需總費用最小？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
