
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若動點![]() 為橢圓
為橢圓![]() 外一點,且點
外一點,且點![]() 到橢圓
到橢圓![]() 的兩條切線相互垂直,求點
的兩條切線相互垂直,求點![]() 的軌跡方程.
的軌跡方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)利用題中條件求出![]() 的值,然后根據離心率求出
的值,然后根據離心率求出![]() 的值,最后根據
的值,最后根據![]() 、
、![]() 、
、![]() 三者的關系求出
三者的關系求出![]() 的值,從而確定橢圓
的值,從而確定橢圓![]() 的標準方程;(2)分兩種情況進行計算:第一種是在從點
的標準方程;(2)分兩種情況進行計算:第一種是在從點![]() 所引的兩條切線的斜率都存在的前提下,設兩條切線的斜率分別為
所引的兩條切線的斜率都存在的前提下,設兩條切線的斜率分別為![]() 、
、![]() ,并由兩條切線的垂直關系得到
,并由兩條切線的垂直關系得到![]() ,并設從點
,并設從點![]() 所引的直線方程為
所引的直線方程為![]() ,將此直線的方程與橢圓的方程聯立得到關于
,將此直線的方程與橢圓的方程聯立得到關于![]() 的一元二次方程,利用
的一元二次方程,利用![]() 得到有關
得到有關![]() 的一元二次方程,最后利用
的一元二次方程,最后利用![]() 以及韋達定理得到點
以及韋達定理得到點![]() 的軌跡方程;第二種情況是兩條切線與坐標軸垂直的情況下求出點
的軌跡方程;第二種情況是兩條切線與坐標軸垂直的情況下求出點![]() 的坐標,并驗證點
的坐標,并驗證點![]() 是否在第一種情況下所得到的軌跡上,從而得到點
是否在第一種情況下所得到的軌跡上,從而得到點![]() 的軌跡方程.
的軌跡方程.
(1)由題意知![]() ,且有
,且有![]() ,即
,即![]() ,解得
,解得![]() ,
,
因此橢圓![]() 的標準方程為
的標準方程為![]() ;
;
(2)①設從點![]() 所引的直線的方程為
所引的直線的方程為![]() ,即
,即![]() ,
,
當從點![]() 所引的橢圓
所引的橢圓![]() 的兩條切線的斜率都存在時,分別設為
的兩條切線的斜率都存在時,分別設為![]() 、
、![]() ,則
,則![]() ,
,
將直線![]() 的方程代入橢圓
的方程代入橢圓![]() 的方程并化簡得
的方程并化簡得![]() ,
,
![]() ,
,
化簡得![]() ,即
,即![]() ,
,
則![]() 、
、![]() 是關于
是關于![]() 的一元二次方程
的一元二次方程![]() 的兩根,則
的兩根,則![]() ,
,
化簡得![]() ;
;
②當從點![]() 所引的兩條切線均與坐標軸垂直,則
所引的兩條切線均與坐標軸垂直,則![]() 的坐標為
的坐標為![]() ,此時點
,此時點![]() 也在圓
也在圓![]() 上.
上.
綜上所述,點![]() 的軌跡方程為
的軌跡方程為![]() .
.


科目:高中數學 來源: 題型:
【題目】設a∈R,函數f(x)=x|x﹣a|+2x.
(1)若a=2,求函數f(x)在區間[0,3]上的最大值;
(2)若a>2,寫出函數f(x)的單調區間(不必證明);
(3)若存在a∈[﹣2,4],使得關于x的方程f(x)=tf(a)有三個不相等的實數解,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)某工廠某種產品的年固定成本為250萬元,每生產![]() 千件,需另投入成本為
千件,需另投入成本為![]() ,當年產量不足80千件時,
,當年產量不足80千件時,![]() (萬元).當年產量不小于80千件時,
(萬元).當年產量不小于80千件時,![]() (萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.(Ⅰ)寫出年利潤
(萬元).每件商品售價為0.05萬元.通過市場分析,該廠生產的商品能全部售完.(Ⅰ)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (千件)的函數解析式;
(千件)的函數解析式;
(Ⅱ)年產量為多少千件時,該廠在這一商品的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數 ![]() 是偶函數,求解下列問題.
是偶函數,求解下列問題.
(1)求θ;
(2)將函數y=f(x)的圖象先縱坐標不變,橫坐標縮短為原來的 ![]() 倍,再向左平移
倍,再向左平移 ![]() 個單位,然后向上平移1個單位得到y=g(x)的圖象,若關于x的方程
個單位,然后向上平移1個單位得到y=g(x)的圖象,若關于x的方程 ![]() 在
在 ![]() 有且只有兩個不同的根,求m的范圍.
有且只有兩個不同的根,求m的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(a,cos2x),
=(a,cos2x), ![]() =(1+sin2x ,
=(1+sin2x , ![]() ),x∈R,記f(x)=
),x∈R,記f(x)= ![]()
![]() .若y=f(x)的圖象經過點(
.若y=f(x)的圖象經過點( ![]() ,2 ).
,2 ).
(1)求實數a的值;
(2)設x∈[﹣ ![]() ,
, ![]() ],求f(x)的最大值和最小值;
],求f(x)的最大值和最小值;
(3)將y=f(x)的圖象向右平移 ![]() ,再將得到的圖象上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到y=g(x)的圖象,求y=g(x)的單調遞減區間.
,再將得到的圖象上各點的橫坐標伸長到原來的4倍,縱坐標不變,得到y=g(x)的圖象,求y=g(x)的單調遞減區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查觀眾對某電視劇的喜愛程度,某電視臺在甲乙兩地隨機抽取了8名觀眾做問卷調查,得分結果如圖所示:
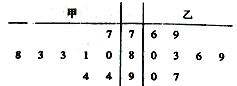
(1)計算甲地被抽取的觀眾問卷得分的中位數和乙地被抽取的觀眾問卷得分的平均數;
(2)若從乙地被抽取的8名觀眾中邀請2人參加調研,求參加調研的觀眾中恰有1人的問卷調查成績在90分以上(含90分)的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線C的極坐標方程是ρ=4cosθ.以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直l的參數方程是![]() (t是參數)
(t是參數)
(1)將曲線C的極坐標方程化為直角坐標方程;
(2)若直線l與曲線C相交于A、B兩點,且|AB|=![]() ,求直線的傾斜角α的值.
,求直線的傾斜角α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的有 . (寫出所有正確說法的序號) ①已知關于x的不等式mx2+mx+2>0的角集為R,則實數m的取值范圍是0<m<4.
②已知等比數列{an}的前n項和為Sn , 則Sn、S2n﹣Sn、S3n﹣S2n也構成等比數列.
③已知函數 ![]() (其中a>0且a≠1)在R上單調遞減,且關于x的方程
(其中a>0且a≠1)在R上單調遞減,且關于x的方程 ![]() 恰有兩個不相等的實數解,則
恰有兩個不相等的實數解,則 ![]() .
.
④已知a>0,b>﹣1,且a+b=1,則 ![]() +
+ ![]() 的最小值為
的最小值為 ![]() .
.
⑤在平面直角坐標系中,O為坐標原點,| ![]() |=|
|=| ![]() |=|
|=| ![]() |=1,
|=1, ![]() +
+ ![]() +
+ ![]() =
= ![]() ,A(1,1),則
,A(1,1),則 ![]() 的取值范圍是
的取值范圍是 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1:y=cosx,C2:y=sin(2x+![]() ),則下面結論正確的是( )
),則下面結論正確的是( )
A. 把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
B. 把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
C. 把C1上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向右平移
倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
D. 把C1上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向左平移
倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com