
如圖,M—l—N是120°的二面角,A、B兩點在棱上,AB=2,D在平面M內,三角形ABD是等腰直角三角形,∠DAB=90°,C在N內,三角形ABC是直角三角形,∠ACB=90°,∠ABC=60°.
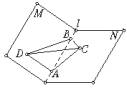
(1)求三棱錐D—ABC的體積;
(2)求直線BD與平面N所成的角的正弦值;
(3)求二面角D—AC—B的平面角的正切值.
答案:解:(1)過D向平面N作垂線,垂足為O,連接OA并延長至E. ∵AB⊥AD,OA為DA在平面N內的射影, ∴AB⊥OA.∴∠DAE為二面角M—l—N的平面角. ∴∠DAE=120°.∴∠DAO=60°. ∵AD=AB=2,∴ ∵△ABC是有一個銳角為30°的直角三角形,斜邊AB=2, ∴ ∴ (2)由(1)可知,∠DBO為直線BD與平面N所成的角, ∴ (3)過O在N內作OF⊥AC,交AC的反向延長線于F,連接DF,則AC⊥DF, ∴∠DFO為二面角D—AC—B的平面角.又在△DOA中,OA=2cos60°=1,即∠OAF= ∠EOC=60°,∴OF=1·sin60°= ∴
|


科目:高中數學 來源: 題型:
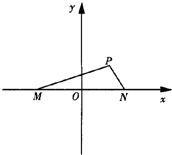 如圖,已知在坐標平面內,M、N是x軸上關于原點O對稱的兩點,P是上半平面內一點,△PMN的面積為
如圖,已知在坐標平面內,M、N是x軸上關于原點O對稱的兩點,P是上半平面內一點,△PMN的面積為| 3 |
| 2 |
| 3 |
| ||
| 2 |
| MP |
| OA |
| MN |
| OP |
| MN |
| CD |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知橢圓C的中心在坐標原點,焦點在x軸上,左、右焦點分別為F1,F2,且|F1F2|=2,點P(1,
已知橢圓C的中心在坐標原點,焦點在x軸上,左、右焦點分別為F1,F2,且|F1F2|=2,點P(1,| 3 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖:過拋物線y2=4x上的點A(1,2)作切線l交x軸與直線x=-4分別于D,B.動點P是拋物線y2=4x上的一點,點E在線段AP上,滿足
如圖:過拋物線y2=4x上的點A(1,2)作切線l交x軸與直線x=-4分別于D,B.動點P是拋物線y2=4x上的一點,點E在線段AP上,滿足| AE |
| EP |
| BF |
| FP |
查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:044

(1)求三棱錐D—ABC的體積;
(2)求直線BD與平面N所成的角的正弦值;
(3)求二面角D—AC—B的平面角的正切值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com