
【題目】設圓x2+y2+2x-15=0的圓心為A,直線l過點B(1,0)且與x軸不重合,l交圓A于C,D兩點,過B作AC的平行線交AD于點E.
(1)證明|EA|+|EB|為定值,并寫出點E的軌跡方程;
(2)設點E的軌跡為曲線C1,直線l交C1于M,N兩點,過B且與l垂直的直線與圓A交于P,Q兩點,求四邊形MPNQ面積的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】試題分析:(1)根據圖形中圓的半徑相等及平行線同位角相等容易得出EB=ED,得出結論|EA|+|EB|為定值,利用定義可以判斷出點E的軌跡為橢圓,求出方程,但要注意標注范圍;(2)求對角線互相垂直的四邊形面積的最值,首先設直線方程聯立方程組求弦長,表示出四邊形的面積,再求出面積的最值,注意直線的斜率不存在的情形.
試題解析:
(1)∵|AD|=|AC|,EB∥AC,故∠EBD=∠ACD=∠ADC,
∴|EB|=|ED|,
故|EA|+|EB|=|EA|+|ED|=|AD|.
又圓A的標準方程為(x+1)2+y2=16,
從而|AD|=4.
∴|EA|+|EB|=4.
由題設得A(-1,0),B(1,0),|AB|=2,
由橢圓定義可得點E的跡方程為:![]() (y≠0).
(y≠0).
(2)當l與x軸不垂直時,設l的方程為y=k(x-1)(k≠0),M(x1,y1),N(x2,y2).
由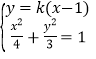
得(4k2+3)x2-8k2x+4k2-12=0.
則x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
∴|MN|=![]() |x1-x2|=
|x1-x2|=![]() .
.
過點B(1,0)且與l垂直的直線m:
y=-![]() (x-1),A到m的距離為
(x-1),A到m的距離為![]() ,
,
∴|PQ|=2![]() .
.
故四邊形MPNQ的面積
S=![]() |MN||PQ|=12
|MN||PQ|=12![]() .
.
可得當l與x軸不垂直時,四邊形MPNQ面積的取值范圍為[12,8![]() ).
).
當l與x軸垂直時,其方程為x=1,|MN|=3,|PQ|=8,四邊形MPNQ的面積為12.
綜上,四邊形MPNQ面積的取值范圍為[12,8![]() ).
).


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區甲、乙、丙三所單位進行招聘,其中甲單位招聘2名,乙單位招聘2名,丙單位招聘1名,并且甲單位要至少招聘一名男生,現有3男3女參加三所單位的招聘,則不同的錄取方案種數為( )
A.36B.72C.108D.144
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求
時,求![]() 的極值;
的極值;
(2)是否存在實數![]() ,使得
,使得![]() 與
與![]() 的單調區間相同,若存在,求出
的單調區間相同,若存在,求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(3)若![]() ,求證:
,求證:![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐S﹣ABCD中,M是SB的中點,AB∥CD,BC⊥CD,且AB=BC=2,CD=SD=1,又SD⊥面SAB.
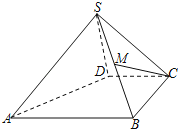
(1)證明:CD⊥SD;
(2)證明:CM∥面SAD;
(3)求四棱錐S﹣ABCD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 與直線
與直線![]() 相切于點
相切于點![]() ,圓心
,圓心![]() 在
在![]() 軸上.
軸上.
(1)求圓![]() 的方程;
的方程;
(2)過點![]() 且不與
且不與![]() 軸重合的直線
軸重合的直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,
兩點,![]() 為坐標原點,直線
為坐標原點,直線![]() 分別與直線
分別與直線![]() 相交于
相交于![]() 兩點,記
兩點,記![]() ,
,![]() 的面積分別是
的面積分別是![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com