
已知函數(shù) ,其中
,其中 為常數(shù).
為常數(shù).
(1)當 時,求函數(shù)
時,求函數(shù) 的單調(diào)遞增區(qū)間;
的單調(diào)遞增區(qū)間;
(2)若任取 ,求函數(shù)
,求函數(shù) 在
在 上是增函數(shù)的概率.
上是增函數(shù)的概率.
(Ⅰ)函數(shù) 的單調(diào)遞增區(qū)間分別為
的單調(diào)遞增區(qū)間分別為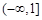 和
和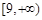 ;(Ⅱ)函數(shù)
;(Ⅱ)函數(shù) 在
在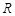 上是增函數(shù)的概率為
上是增函數(shù)的概率為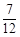 .
.
解析試題分析:(Ⅰ)求函數(shù) 的單調(diào)遞增區(qū)間,首先將
的單調(diào)遞增區(qū)間,首先將 代入,我們易求出函數(shù)的解析式,從而求出函數(shù)的導函數(shù)后,令導函數(shù)的函數(shù)值大于等于0,由此構造關于
代入,我們易求出函數(shù)的解析式,從而求出函數(shù)的導函數(shù)后,令導函數(shù)的函數(shù)值大于等于0,由此構造關于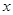 的不等式,解不等式即可得到函數(shù)
的不等式,解不等式即可得到函數(shù) 的單調(diào)遞增區(qū)間;(Ⅱ)求函數(shù)
的單調(diào)遞增區(qū)間;(Ⅱ)求函數(shù) 在
在 上是增函數(shù)的概率,這是一個幾何概型問題,我們可以先畫出
上是增函數(shù)的概率,這是一個幾何概型問題,我們可以先畫出 ,對應的平面區(qū)域的面積,然后再求出滿足條件函數(shù)
,對應的平面區(qū)域的面積,然后再求出滿足條件函數(shù) 在
在 上是增函數(shù)時對應的平面區(qū)域的面積,計算出對應的面積后,代入幾何概型公式即可得到答案.
上是增函數(shù)時對應的平面區(qū)域的面積,計算出對應的面積后,代入幾何概型公式即可得到答案.
試題解析:(1)當 時,
時, ,
,
令 ,
, ,解得
,解得 或
或 ,
,
故函數(shù) 的單調(diào)遞增區(qū)間分別為
的單調(diào)遞增區(qū)間分別為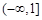 和
和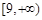
(2)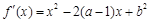
若函數(shù) 在
在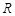 上是增函數(shù),則對于任意
上是增函數(shù),則對于任意 ,
,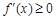 恒成立.
恒成立.
所以,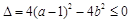 ,即
,即 8分
8分
設“ 在
在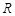 上是增函數(shù)”為事件
上是增函數(shù)”為事件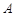 ,則事件
,則事件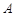 對應的區(qū)域為
對應的區(qū)域為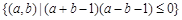
全部試驗結果構成的區(qū)域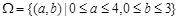 ,
,
所以,
故函數(shù) 在
在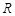 上是增函數(shù)的概率為
上是增函數(shù)的概率為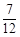
考點:利用導數(shù)研究函數(shù)的單調(diào)性;幾何概型;概率的應用.


科目:高中數(shù)學 來源: 題型:解答題
已知a,b為常數(shù),a¹0,函數(shù) .
.
(1)若a=2,b=1,求 在(0,+∞)內(nèi)的極值;
在(0,+∞)內(nèi)的極值;
(2)①若a>0,b>0,求證: 在區(qū)間[1,2]上是增函數(shù);
在區(qū)間[1,2]上是增函數(shù);
②若 ,
, ,且
,且 在區(qū)間[1,2]上是增函數(shù),求由所有點
在區(qū)間[1,2]上是增函數(shù),求由所有點 形成的平面區(qū)域的面積.
形成的平面區(qū)域的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù) =
= 。
。
(1)當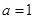 時,求函數(shù)
時,求函數(shù) 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(2)求函數(shù) 在區(qū)間
在區(qū)間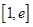 上的最小值;
上的最小值;
(3)在(1)的條件下,設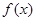 =
= +
+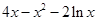 ,
,
求證: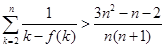 (
(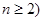 ),參考數(shù)據(jù):
),參考數(shù)據(jù):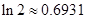 。(13分)
。(13分)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知 .
.
(1)曲線y=f(x)在x=0處的切線恰與直線 垂直,求
垂直,求 的值;
的值;
(2)若x∈[a,2a]求f(x)的最大值;
(3)若f(x1)=f(x2)=0(x1<x2),求證: .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某市在市內(nèi)主干道北京路一側(cè)修建圓形休閑廣場.如圖,圓形廣場的圓心為O,半徑為100m,并與北京路一邊所在直線 相切于點M.A為上半圓弧上一點,過點A作
相切于點M.A為上半圓弧上一點,過點A作 的垂線,垂足為B.市園林局計劃在△ABM內(nèi)進行綠化.設△ABM的面積為S(單位:
的垂線,垂足為B.市園林局計劃在△ABM內(nèi)進行綠化.設△ABM的面積為S(單位: ),
), (單位:弧度).
(單位:弧度).
(I)將S表示為 的函數(shù);
的函數(shù);
(II)當綠化面積S最大時,試確定點A的位置,并求最大面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某建筑公司要在一塊寬大的矩形地面(如圖所示)上進行開發(fā)建設,陰影部分為一公共設施不能建設開發(fā),且要求用欄柵隔開(欄柵要求在直線上),公共設施邊界為曲線 的一部分,欄柵與矩形區(qū)域的邊界交于點M、N,切曲線于點P,設
的一部分,欄柵與矩形區(qū)域的邊界交于點M、N,切曲線于點P,設 .
.
(I)將 (O為坐標原點)的面積S表示成f的函數(shù)S(t);
(O為坐標原點)的面積S表示成f的函數(shù)S(t);
(II)若 ,S(t)取得最小值,求此時a的值及S(t)的最小值.
,S(t)取得最小值,求此時a的值及S(t)的最小值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com