【題目】(本小題滿分12分)
已知關于
的不等式
，其中
.
（1）當
變化時，試求不等式的解集
；
（2）對于不等式的解集，若滿足
（其中
為整數集）. 試探究集合
能否為有限集？若 能，求出使得集合中元素個數最少的的所有取值，并用列舉法表示集合；若不能，請說明理由.
科目：高中數學 來源： 題型：
【題目】四棱錐
中， 
面
， 
是平行四邊形， 
， 
，點
為棱
的中點，點
在棱
上，且
，平面
與
交于點
，則異面直線
與
所成角的正切值為__________．
【答案】
【解析】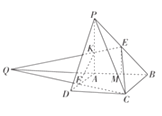
延長
交
的延長線與點Q，連接QE交PA于點K，設QA=x，
由
，得
，則
，所以
.
取
的中點為M,連接EM，則
，
所以
，則
，所以AK=
.
由AD//BC，得異面直線
與
所成角即為
,
則異面直線
與
所成角的正切值為
.
【題型】填空題
【結束】
17
【題目】在極坐標系中，極點為
，已知曲線
： 
與曲線
： 
交于不同的兩點
， 
．
（1）求
的值；
（2）求過點
且與直線
平行的直線
的極坐標方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知下列命題：
①命題：x∈（0，2），3x＞x3的否定是：x∈（0，2），3x≤x3；
②若f（x）=2x﹣2﹣x ， 則x∈R，f（﹣x）=﹣f（x）；
③若f（x）=x+ 
，則x0∈（0，+∞），f（x0）=1；
④等差數列{an}的前n項和為Sn ， 若a4=3，則S7=21；
⑤在△ABC中，若A＞B，則sinA＞sinB．
其中真命題是 ． （只填寫序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，建立平面直角坐標系，x軸在地平面上，y軸垂直于地平面，單位長度為1 km，某炮位于原點．已知炮彈發射后的軌跡在方程y＝kx－
(1＋k2)x2(k＞0)表示的曲線上，其中k與發射方向有關．炮的射程是指炮彈落地點的橫坐標．則炮的最大射程為( )
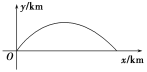
A. 20 km B. 10 km
C. 5 km D. 15 km
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，∠BAD= 
，AB=2，AD=1，若M、N分別是邊AD、CD上的點，且滿足 
=λ，其中λ∈[0，1]，則 
的取值范圍是（ ） 
A.[﹣3，﹣1]
B.[﹣3，1]
C.[﹣1，1]
D.[1，3]
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在數列
中，已知
，對于任意的
，有
.
（1）求數列的通項公式.
（2）若數列
滿足
，求數列的通項公式.
（3）設
，是否存在實數
，當
時，
恒成立？若存在，求實數的取值范圍；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設f（x）= 
（x＞0），計算觀察以下格式： f1（x）=f（x），f2（x）=f（f1（x）），f3（x）=f（f2（x）），f4（x）=f（f3（x）），…
根據以上事實得到當n∈N*時，fn（1）= ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知一次函數f(x)＝ax－2.
(1)當a＝3時，解不等式|f(x)|＜4；
(2)解關于x的不等式|f(x)|＜4；
(3)若關于x的不等式|f(x)|≤3對任意x∈[0,1]恒成立，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖,小明想將短軸長為2,長軸長為4的一個半橢圓形紙片剪成等腰梯形ABDE,且梯形ABDE內接于半橢圓,DE∥AB,AB為短軸,OC為長半軸
(1)求梯形ABDE上底邊DE與高OH長的關系式;
(2)若半橢圓上到H的距離最小的點恰好為C點,求底邊DE的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
