
【題目】某校要在一條水泥路邊安裝路燈,其中燈桿的設計如圖所示,AB為地面,CD,CE為路燈燈桿,CD⊥AB,∠DCE=![]() ,在E處安裝路燈,且路燈的照明張角∠MEN=
,在E處安裝路燈,且路燈的照明張角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
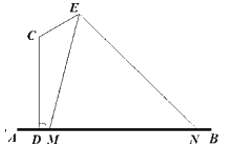
(1)當M,D重合時,求路燈在路面的照明寬度MN;
(2)求此路燈在路面上的照明寬度MN的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知圓O:x2+y2=3上的一動點M在x軸上的投影為N,點P滿足![]() .
.
(1)求動點P的軌跡C的方程;
(2)若直線l與圓O相切,且交曲線C于點A,B,試求|AB|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某景區內有一半圓形花圃,其直徑AB為6,O是圓心,且OC⊥AB.在OC上有一座觀賞亭Q,其中∠AQC=![]() ,.計劃在
,.計劃在![]() 上再建一座觀賞亭P,記∠POB=θ
上再建一座觀賞亭P,記∠POB=θ![]() .
.
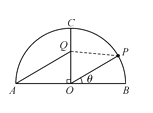
(1)當θ=![]() 時,求∠OPQ的大小;
時,求∠OPQ的大小;
(2)當∠OPQ越大時,游客在觀賞亭P處的觀賞效果越佳,求游客在觀賞亭P處的觀賞效果最佳時,角θ的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公園內有一塊以![]() 為圓心半徑為
為圓心半徑為![]() 米的圓形區域.為豐富市民的業余文化生活,現提出如下設計方案:如圖,在圓形區域內搭建露天舞臺,舞臺為扇形
米的圓形區域.為豐富市民的業余文化生活,現提出如下設計方案:如圖,在圓形區域內搭建露天舞臺,舞臺為扇形![]() 區域,其中兩個端點
區域,其中兩個端點![]() ,
,![]() 分別在圓周上;觀眾席為梯形
分別在圓周上;觀眾席為梯形![]() 內切在圓
內切在圓![]() 外的區域,其中
外的區域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在點
在點![]() 的同側.為保證視聽效果,要求觀眾席內每一個觀眾到舞臺
的同側.為保證視聽效果,要求觀眾席內每一個觀眾到舞臺![]() 處的距離都不超過
處的距離都不超過![]() 米.設
米.設![]() ,
,![]() .問:對于任意
.問:對于任意![]() ,上述設計方案是否均能符合要求?
,上述設計方案是否均能符合要求?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市2010年4月1日—4月30日對空氣污染指數的監測數據如(主要污染物為可吸入顆粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
樣本頻率分布表:
分組 | 頻數 | 頻率 |
[41,51) | 2 | |
[51,61) | 1 | |
[61,71) | 4 | |
[71,81) | 6 | |
[81,91) | 10 | |
[91,101) | ||
[101,111) | 2 |
(1) 完成頻率分布表;
(2)作出頻率分布直方圖;
(3)根據國家標準,污染指數在0~50之間時,空氣質量為優:在51~100之間時,為良;在101~150之間時,為輕微污染;在151~200之間時,為輕度污染.請你依據所給數據和上述標準,對該市的空氣質量給出一個簡短評價.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a,b,c分別是角A,B,C的對邊,且acosC=(2b﹣c)cosA.
(1)若![]() 3,求△ABC的面積;
3,求△ABC的面積;
(2)若∠B<∠C,求2cos2B+cos2C的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a,b,c分別為△ABC三個內角A,B,C的對邊,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
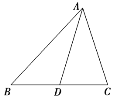
(1)求A;
(2)若AD為BC邊上的中線,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知橢圓![]() 的離心率為
的離心率為![]() ,右準線方程為
,右準線方程為![]() ,
,![]() 、
、![]() 分別是橢圓
分別是橢圓![]() 的左、右頂點,過右焦點
的左、右頂點,過右焦點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
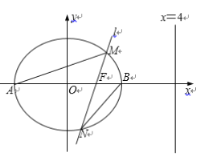
(1)求橢圓![]() 的標準方程.
的標準方程.
(2)記![]() 、
、![]() 的面積分別為
的面積分別為![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)設線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 與右準線相交于點
與右準線相交于點![]() ,記直線
,記直線![]() 、
、![]() 、
、![]() 的斜率分別為
的斜率分別為![]() 、
、![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com