Question

【題目】已知函數(shù)f（x）=2sin2（x+）-2cos（x-）-5a+2．

（1）設(shè)t=sinx+cosx，將函數(shù)f（x）表示為關(guān)于t的函數(shù)g（t），求g（t）的解析式；

（2）對任意x∈[0，]，不等式f（x）≥6-2a恒成立，求a的取值范圍．

Answer 1

【答案】（1），；（2）．

【解析】

試題分析 ：（1）首先由兩角和的正弦公式可得，進(jìn)而即可求出的取值范圍；接下來對已知的函數(shù)利用進(jìn)行表示；

對于（2），首先由的取值范圍，求出的取值范圍，再對已知進(jìn)行恒等變形可得在區(qū)間上恒成立，據(jù)此即可得到關(guān)于的不等式，解不等式即可求出的取值范圍.

試題解析：

（1），

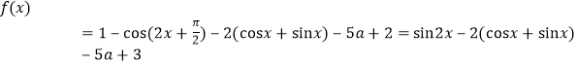因為，所以，其中，

即，．

（2）由（1）知，當(dāng)時，，

又在區(qū)間上單調(diào)遞增，

所以，從而，

要使不等式在區(qū)間上恒成立，只要，

解得：．

點晴:本題考查的是求函數(shù)的解析式及不等式恒成立問題. （1）首先，可求出的取值范圍；接下來對已知的函數(shù)利用進(jìn)行表示;(2)先求二次函數(shù)，再解不等式.