【題目】從2017年1月18日開始，支付寶用戶可以通過“
掃‘福’字”和“參與螞蟻森林”兩種方式獲得福卡（愛國福、富強福、和諧福、友善福，敬業福），除夕夜22:18，每一位提前集齊五福的用戶都將獲得一份現金紅包.某高校一個社團在年后開學后隨機調查了80位該校在讀大學生，就除夕夜22：18之前是否集齊五福進行了一次調查（若未參與集五福的活動，則也等同于未集齊五福），得到具體數據如下表：
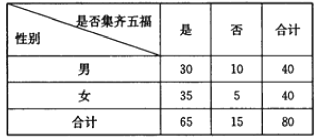
（1）根據如上的列聯表，能否在犯錯誤的概率不超過0.05的前提下，認為“集齊五福與性別有關”？
（2）計算這80位大學生集齊五福的頻率，并據此估算該校10000名在讀大學生中集齊五福的人數；
（3）為了解集齊五福的大學生明年是否愿意繼續參加集五福活動，該大學的學生會從集齊五福的學生中，選取2位男生和3位女生逐個進行采訪，最后再隨機選取3次采訪記錄放到該大學的官方網站上，求最后被選取的3次采訪對象中至少有一位男生的概率.
參考公式：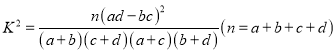 
.
附表：
【答案】（1）不能（2）
，8125（3）
【解析】試題分析：（1）根據列聯表中的數據，得到
的觀測值為
，故得到結果；（2）先得到樣本中集齊五福的頻率為
，再由總人數乘以頻率即可；（3）根據古典概型的計算公式得到，總事件個數為10，滿足條件的事件為9，求得頻率為
.
解析：
（1）根據列聯表中的數據，得到
的觀測值為
，
故不能在犯錯誤的概率不超過0.05的前提下，認為“集齊五福與性別有關”.
（2）這80位大學生集齊五福的頻率為
.
據此估算該校10000名在讀大學生中集齊五福的人數為
.
（3）設選取的2位男生和3位女生分別記為
，隨機選取3次采訪的所有結果為
， 
， 
， 
， 
，共有10個基本事件，至少有一位男生的基本事件有9個，故所求概率為
.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】某工廠利用隨機數表對生產的600個零件進行抽樣測試，先將600個零件進行編號，編號分別為001，002，
，599，600從中抽取60個樣本，如下提供隨機數表的第4行到第6行：
32 21 18 34 29 78 64 54 07 32 52 42 06 44 38 12 23 43 56 77 35 78 90 56 42
84 42 12 53 31 34 57 86 07 36 25 30 07 32 86 23 45 78 89 07 23 68 96 08 04
32 56 78 08 43 67 89 53 55 77 34 89 94 83 75 22 53 55 78 32 45 77 89 23 45
若從表中第6行第6列開始向右依次讀取3個數據，則得到的第6個樣本編號
A. 522B. 324C. 535D. 578
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】過平面直角坐標系中的點P（4-3a，
）（a∈R）作圓x2+y2=1的兩條切線PA，PB，切點分別為A，B，則數量積
的最小值為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，且在
軸上的頂點分別為
，
.
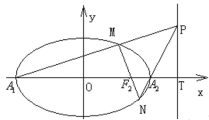
（1）求橢圓的方程；
（2）若直線
與軸交于點
，點
為直線
上異于點的任一點，直線
分別與橢圓交于
點，試問直線
能否通過橢圓的焦點？若能，求出
的值，若不能，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，一張坐標紙上一已作出圓
及點
，折疊此紙片，使
與圓周上某點
重合，每次折疊都會留下折痕，設折痕與直線
的交點為
，令點的軌跡為
.
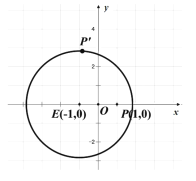
（1）求軌跡的方程；
（2）若直線
與軌跡交于兩個不同的點
，且直線
與以
為直徑的圓相切，若
，求
的面積的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，已知AB丄平面BCD，M、N分別是AC、AD的中點，BC 丄 CD.
（1）求證：MN//平面BCD；
（2）若AB=1，BC=
，求直線AC與平面BCD所成的角.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某城市的電視發射搭CD建在市郊的一座小山上，如圖所示，小山高BC為30米，在地平面上有一點A，測得A，C兩點間距離為50米.
（1）如果從點A觀測電視發射塔的視角∠CAD=
，求這座電視發射塔的高度；
（2）點A在何位置時，角∠CAD最大.（參考數據：
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分13分）如圖所示的莖葉圖記錄了甲、乙兩組各四名同學的投籃命中次數, 乙組記錄中有一個數據模糊，無法確認, 在圖中以
表示.
（Ⅰ）如果乙組同學投籃命中次數的平均數為
, 求及乙組同學投籃命中次數的方差;
（Ⅱ）在（Ⅰ）的條件下, 分別從甲、乙兩組投籃命中次數低于10次的同學中,各隨機選取一名, 記事件A：“兩名同學的投籃命中次數之和為17”, 求事件A發生的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2017年“十一”期間，高速公路車輛較多．某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查，將他們在某段高速公路的車速（
）分成六段： 
， 
， 
， 
， 
， 
，后得到如圖的頻率分布直方圖．
（1）求這40輛小型車輛車速的眾數和中位數的估計值；
（2）若從車速在
的車輛中任抽取2輛，求車速在的車輛恰有一輛的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com