
(本小題滿分10分)已知函數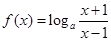 .
.
(1)求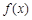 的定義域;(2)判斷
的定義域;(2)判斷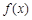 的奇偶性并證明;
的奇偶性并證明;
(1)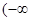 ,
,  ,
, 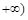 ;(2)見解析。
;(2)見解析。
解析試題分析:(1)∵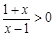 ∴
∴ 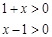 或
或 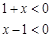 ,∴定義域為
,∴定義域為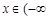 ,
,  ,
, 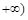 .---5分
.---5分
(2)由(1)知函數的定義域為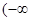 ,
,  ,
, 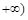 ,關于原點對稱,
,關于原點對稱,
又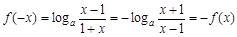 ,∴
,∴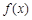 為奇函數.----10分
為奇函數.----10分
考點:本題考查函數定義域的求法;函數奇偶性的判斷及證明;分式不等式的解法。
點評:在函數奇偶性的定義中,有兩個必備條件:一是定義域關于原點對稱,這是函數具有奇偶性的必要不充分條件,所以首先考慮定義域對解決問題是有利的;二是判斷f(x)與f(-x)是否具有等量關系.在判斷奇偶性的運算中,可以轉化判斷奇偶性的等價等量關系式為f(x)+f(-x)=0(奇函數)或f(x)-f(-x)=0(偶函數)是否成立,這樣能簡化計算。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分13分)
某商場根據調查,估計家電商品從年初(1月)開始的 個月內累計的需求量
個月內累計的需求量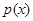 (百件)為
(百件)為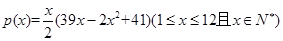
(1)求第 個月的需求量
個月的需求量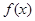 的表達式.
的表達式.
(2)若第 個月的銷售量滿足
個月的銷售量滿足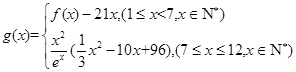 (單位:百件),每件利潤
(單位:百件),每件利潤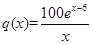 元,求該商場銷售該商品,求第幾個月的月利潤達到最大值?最大是多少?
元,求該商場銷售該商品,求第幾個月的月利潤達到最大值?最大是多少? 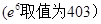
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分12分) 已知函數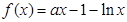
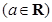 .
.
(1)討論函數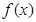 在定義域內的極值點的個數;
在定義域內的極值點的個數;
(2)若函數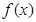 在
在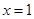 處取得極值,對
處取得極值,對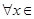
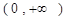 ,
,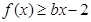 恒成立,求實數
恒成立,求實數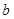 的取值范圍;
的取值范圍;
(3)當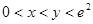 且
且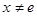 時,試比較
時,試比較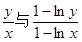 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
2013年全國第十二屆全運會由沈陽承辦。城建部門計劃在渾南新區建造一個長方形公園ABCD,公園由長方形的休閑區A1B1C1D1(陰影部分)和環公園人行道組成。已知休閑區A1B1C1D1的面積為4000平方米,人行道的寬分別為4米和10米。
(1)若設休閑區的長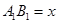 米,求公園ABCD所占面積S關于
米,求公園ABCD所占面積S關于 的函數
的函數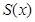 的解析式;
的解析式;
(2)要使公園所占面積最小,休閑區A1B1C1D1的長和寬該如何設計?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)設某物體一天中的溫度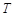 是時間
是時間 的函數:
的函數: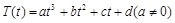 ,其中溫度的單位是
,其中溫度的單位是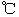 ,時間單位是小時,
,時間單位是小時,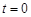 表示12:00,
表示12:00, 取正值表示12:00以后.若測得該物體在8:00的溫度是
取正值表示12:00以后.若測得該物體在8:00的溫度是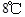 ,12:00的溫度為
,12:00的溫度為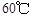 ,13:00的溫度為
,13:00的溫度為 ,且已知該物體的溫度在8:00和16:00有相同的變化率.
,且已知該物體的溫度在8:00和16:00有相同的變化率.
(1)寫出該物體的溫度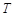 關于時間
關于時間 的函數關系式;
的函數關系式;
(2)該物體在10:00到14:00這段時間中(包括10:00和14:00),何時溫度最高,并求出最高溫度;
(3)如果規定一個函數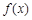 在區間
在區間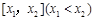 上的平均值為
上的平均值為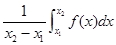 ,求該物體在8:00到16:00這段時間內的平均溫度.
,求該物體在8:00到16:00這段時間內的平均溫度.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(10分)某公司生產一種電子儀器的固定成本為20000元,每生產一臺儀器需增加投入100元,已知總收益滿足函數:
R(x)=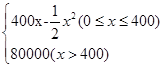 .
.
其中x是儀器的月產量.
(1)將利潤表示為月產量的函數f(x);
(2)當月產量為何值時,公司所獲利潤最大?最大利潤為多少元?(總收益=總成本+利潤)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com