
【題目】已知數列![]() 的各項均為正數,記數列
的各項均為正數,記數列![]() 的前n項和為
的前n項和為![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)求數列![]() 的通項公式;
的通項公式;
(3)若![]() ,且
,且![]() 成等比數列,求k和t的值.
成等比數列,求k和t的值.
【答案】(1)1(2)![]() .(3)
.(3)![]() .
.
【解析】
(1)令![]() 代入遞推關系,即可求得
代入遞推關系,即可求得![]() 的值;
的值;
(2)連續兩次利用“臨差法”,即多遞推一項再相減,從而構造出![]() 這一遞推關系,再利用等比數列通項公式,即可得答案;
這一遞推關系,再利用等比數列通項公式,即可得答案;
(3)由(2)可知![]() ,由
,由![]() 成等比數列,可得
成等比數列,可得![]() ,即
,即![]() ,再根據等式兩邊奇、偶數的特點,推理得到k和t的值.
,再根據等式兩邊奇、偶數的特點,推理得到k和t的值.
(1)由![]() ,得
,得![]() ,即
,即![]() .
.
因為![]() ,所以
,所以![]() .
.
(2)因為![]() ,①
,①
所以![]() ,②
,②
②-①,得![]() .
.
因為![]() ,
,
所以![]() ,③
,③
所以![]() ,④
,④
④-③,得![]() ,即
,即![]() ,
,
所以當![]() 時,
時,![]() .
.
又由![]() ,得
,得![]() ,
,
即![]() .
.
因為![]() ,所以
,所以![]() ,所以
,所以![]() ,所以對
,所以對![]() ,都有
,都有![]() 成立,
成立,
所以數列![]() 的通項公式為
的通項公式為![]() .
.
(3)由(2)可知![]() .
.
因為![]() 成等比數列,
成等比數列,
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() .
.
由于![]() ,所以
,所以![]() ,即
,即![]() .
.
當![]() 時,
時,![]() ,得
,得![]() .
.
當![]() 時,由
時,由![]() ,得
,得![]() 為奇數,
為奇數,
所以![]() ,即
,即![]() ,代入(*)得
,代入(*)得![]() ,即
,即![]() ,此時k無正整數解.
,此時k無正整數解.
綜上,![]() .
.


科目:高中數學 來源: 題型:
【題目】某校高三(1)班在一次語文測試結束后,發現同學們在背誦內容方面失分較為嚴重.為了提升背誦效果,班主任倡議大家在早、晚讀時間站起來大聲誦讀,為了解同學們對站起來大聲誦讀的態度,對全班50名同學進行調查,將調查結果進行整理后制成下表:
考試分數 |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 5 | 10 | 5 |
贊成人數 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使測試優秀率為30%,則優秀分數線應定為多少分?
(2)依據第1問的結果及樣本數據研究是否贊成站起來大聲誦讀的態度與考試成績是否優秀的關系,列出2×2列聯表,并判斷是否有90%的把握認為贊成與否的態度與成績是否優秀有關系.
參考公式及數據: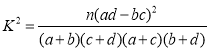 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦點為
的焦點為![]() ,
,![]() ,離心率為
,離心率為![]() ,點P為橢圓C上一動點,且
,點P為橢圓C上一動點,且![]() 的面積最大值為
的面積最大值為![]() ,O為坐標原點.
,O為坐標原點.
(1)求橢圓C的方程;
(2)設點![]() ,
,![]() 為橢圓C上的兩個動點,當
為橢圓C上的兩個動點,當![]() 為多少時,點O到直線MN的距離為定值.
為多少時,點O到直線MN的距離為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,焦距為2,且經過點
,焦距為2,且經過點![]() ,斜率為
,斜率為![]() 的直線
的直線![]() 經過點
經過點![]() ,與橢圓
,與橢圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
(1)求橢圓![]() 的方程;
的方程;
(2)在![]() 軸上是否存在點
軸上是否存在點![]() ,使得以
,使得以![]() ,
,![]() 為鄰邊的平行四邊形是菱形?如果存在,求出
為鄰邊的平行四邊形是菱形?如果存在,求出![]() 的取值范圍,如果不存在,請說明理由.
的取值范圍,如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 與曲線
與曲線![]() ,(
,(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)寫出曲線![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)在極坐標系中,已知![]() 與
與![]() ,
,![]() 的公共點分別為
的公共點分別為![]() ,
,![]() ,
,![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 與拋物線
與拋物線![]() :
:![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() 的面積為16(
的面積為16(![]() 為坐標原點).
為坐標原點).
(1)求![]() 的方程;
的方程;
(2)直線![]() 經過
經過![]() 的焦點
的焦點![]() 且
且![]() 不與
不與![]() 軸垂直,與
軸垂直,與![]() 交于
交于![]() ,
,![]() 兩點,若線段
兩點,若線段![]() 的垂直平分線與
的垂直平分線與![]() 軸交于點
軸交于點![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com