
【題目】2019年是中華人民共和國成立70周年.為了讓人民了解建國70周年的風雨歷程,某地的民調機構隨機選取了該地的100名市民進行調查,將他們的年齡分成6段:![]() ,
,![]() ,…,
,…,![]() ,并繪制了如圖所示的頻率分布直方圖.
,并繪制了如圖所示的頻率分布直方圖.

(1)現從年齡在![]() ,
,![]() ,
,![]() 內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機選取3人進行座談,用
內的人員中按分層抽樣的方法抽取8人,再從這8人中隨機選取3人進行座談,用![]() 表示年齡在
表示年齡在![]() )內的人數,求
)內的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(2)若用樣本的頻率代替概率,用隨機抽樣的方法從該地抽取20名市民進行調查,其中有![]() 名市民的年齡在
名市民的年齡在![]() 的概率為
的概率為![]() .當
.當![]() 最大時,求
最大時,求![]() 的值.
的值.
【答案】(1)分布列見解析,![]()
(2)![]()
【解析】
(1)根據頻率分布直方圖及抽取總人數,結合各組頻率值即可求得各組抽取的人數;![]() 的可能取值為0,1,2,由離散型隨機變量概率求法即可求得各概率值,即可得分布列;由數學期望公式即可求得其數學期望.
的可能取值為0,1,2,由離散型隨機變量概率求法即可求得各概率值,即可得分布列;由數學期望公式即可求得其數學期望.
(2)先求得年齡在![]() 內的頻率,視為概率.結合二項分布的性質,表示出
內的頻率,視為概率.結合二項分布的性質,表示出![]() ,令
,令![]() ,化簡后可證明其單調性及取得最大值時
,化簡后可證明其單調性及取得最大值時![]() 的值.
的值.
(1)按分層抽樣的方法拉取的8人中,
年齡在![]() 的人數為
的人數為![]() 人,
人,
年齡在![]() 內的人數為
內的人數為![]() 人.
人.
年齡在![]() 內的人數為
內的人數為![]() 人.
人.
所以![]() 的可能取值為0,1,2.
的可能取值為0,1,2.
所以![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 的分市列為
的分市列為
| 0 | 1 | 2 |
|
|
|
|
![]() .
.
(2)設在抽取的20名市民中,年齡在![]() 內的人數為
內的人數為![]() ,
,![]() 服從二項分布.由頻率分布直方圖可知,年齡在
服從二項分布.由頻率分布直方圖可知,年齡在![]() 內的頻率為
內的頻率為![]() ,
,
所以![]() ,
,
所以![]() .
.
設![]() ,
,
若![]() ,則
,則![]() ,
,![]() ;
;
若![]() ,則
,則![]() ,
,![]() .
.
所以當![]() 時,
時,![]() 最大,即當
最大,即當![]() 最大時,
最大時,![]() .
.


科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知圓
中,已知圓![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).以
為參數).以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() :
:![]() 與圓
與圓![]() 的交點為
的交點為![]() 、
、![]() 兩點,
兩點,![]() 與直線
與直線![]() 的交點為
的交點為![]() .
.
(1)求圓![]() 的極坐標方程;
的極坐標方程;
(2)求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,側面
中,側面![]() ⊥底面
⊥底面![]() ,底面
,底面![]() 為直角梯形,
為直角梯形,![]() //
//![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.

(Ⅰ)求證:PA//平面BEF;
(Ⅱ)若PC與AB所成角為![]() ,求
,求![]() 的長;
的長;
(Ⅲ)在(Ⅱ)的條件下,求二面角F-BE-A的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是民航部門統計的某年春節期間:中國民航出入境航線方面TOP10出入境國家和地區的旅客量以及相比上年同期變化幅度的數據統計圖表,根據圖表,下面敘述不正確的是( )
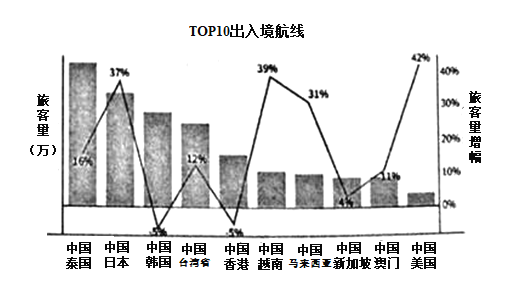
A.東南亞仍是人們出境旅游的首選
B.臺灣和澳門均有超過一成的同比增長
C.越南和美國排在人們出境旅游選擇的前兩位
D.中-韓航線雖依然位列出入境國家和地區第三甲,但旅客量卻較去年出現負增長
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】植物園擬建一個多邊形苗圃,苗圃的一邊緊靠著長度大于30m的圍墻.現有兩種方案:
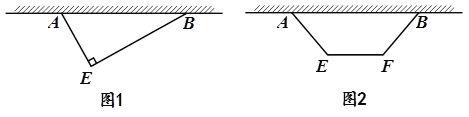
方案① 多邊形為直角三角形![]() (
(![]() ),如圖1所示,其中
),如圖1所示,其中![]() ;
;
方案② 多邊形為等腰梯形![]() (
(![]() ),如圖2所示,其中
),如圖2所示,其中![]() .
.
請你分別求出兩種方案中苗圃的最大面積,并從中確定使苗圃面積最大的方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年全球爆發新冠肺炎,人感染了新冠肺炎病毒后常見的呼吸道癥狀有:發熱、咳嗽、氣促和呼吸困難等,嚴重時會危及生命.隨著疫情的發展,自2020年2月5日起,武漢大面積的爆發新冠肺炎,政府為了及時收治輕癥感染的群眾,逐步建立起了14家方艙醫院,其中武漢體育中心方艙醫院從2月12日開艙至3月8日閉倉,累計收治輕癥患者1056人.據部分統計該方艙醫院從2月26日至3月2日輕癥患者治愈出倉人數的頻數表與散點圖如下:
日期 | 2.26 | 2.27 | 2.28 | 2.29 | 3.1 | 3.2 |
序號 | 1 | 2 | 3 | 4 | 5 | 6 |
出倉人數 | 3 | 8 | 17 | 31 | 68 | 168 |

根據散點圖和表中數據,某研究人員對出倉人數![]() 與日期序號
與日期序號![]() 進行了擬合分析.從散點圖觀察可得,研究人員分別用兩種函數①
進行了擬合分析.從散點圖觀察可得,研究人員分別用兩種函數①![]() ②
②![]() 分析其擬合效果.其相關指數
分析其擬合效果.其相關指數![]() 可以判斷擬合效果,R2越大擬合效果越好.已知
可以判斷擬合效果,R2越大擬合效果越好.已知![]() 的相關指數為
的相關指數為![]() .
.
(1)試根據相關指數判斷.上述兩類函數,哪一類函數的擬合效果更好?(注:相關系數![]() 與相關指數R2滿足
與相關指數R2滿足![]() ,參考數據表中
,參考數據表中![]() )
)
(2)①根據(1)中結論,求擬合效果更好的函數解析式;(結果保留小數點后三位)
②3月3日實際總出倉人數為216人,按①中的回歸模型計算,差距有多少人?
(附:對于一組數據![]() ,其回歸直線為
,其回歸直線為![]()
相關系數
參考數據:
|
|
|
|
|
|
|
|
|
3.5 | 49.17 | 15.17 | 3.13 | 894.83 | 19666.83 | 10.55 | 13.56 | 3957083 |
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】垃圾分類,是指按一定規定或標準將垃圾分類儲存、分類投放和分類搬運,從而轉變成公共資源的一系列活動的總稱.分類的目的是提高垃圾的資源價值和經濟價值,力爭物盡其用.2019年6月25日,生活垃圾分類制度入法.到2020年底,先行先試的46個重點城市,要基本建成垃圾分類處理系統;其他地級城市實現公共機構生活垃圾分類全覆蓋.某機構欲組建一個有關“垃圾分類”相關事宜的項目組,對各個地區“垃圾分類”的處理模式進行相關報道.該機構從600名員工中進行篩選,篩選方法:每位員工測試![]() ,
,![]() ,
,![]() 三項工作,3項測試中至少2項測試“不合格”的員工,將被認定為“暫定”,有且只有一項測試“不合格”的員工將再測試
三項工作,3項測試中至少2項測試“不合格”的員工,將被認定為“暫定”,有且只有一項測試“不合格”的員工將再測試![]() ,
,![]() 兩項,如果這兩項中有1項以上(含1項)測試“不合格”,將也被認定為“暫定”,每位員工測試
兩項,如果這兩項中有1項以上(含1項)測試“不合格”,將也被認定為“暫定”,每位員工測試![]() ,
,![]() ,
,![]() 三項工作相互獨立,每一項測試“不合格”的概率均為
三項工作相互獨立,每一項測試“不合格”的概率均為![]() .
.
(1)記某位員工被認定為“暫定”的概率為![]() ,求
,求![]() ;
;
(2)每位員工不需要重新測試的費用為90元,需要重新測試的總費用為150元,除測試費用外,其他費用總計為1萬元,若該機構的預算為8萬元,且該600名員工全部參與測試,問上述方案是否會超過預算?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com