【題目】已知曲線
為參數），
為參數）.
（1）化
的參數方程為普通方程，并說明它們分別表示什么曲線；
（2）若
上的點
對應的參數為
為
上的動點，求
的中點
到直線
為參數）距離的最小值.
【答案】（1）C1：（x+4）2+（y﹣3）2=1；C2：
，（2）點Q（
，﹣
）
【解析】試題分析：（1）分別消去兩曲線參數方程中的參數得到兩曲線的直角坐標方程，即可得到曲線
表示一個圓；曲線
表示一個橢圓；（2）把
的值代入曲線
的參數方程得點
的坐標，然后把直線的參數方程化為普通方程，根據曲線
的參數方程設出
的坐標，利用中點坐標公式表示出
的坐標，利用點到直線的距離公式標準處
到已知直線的距離，利用兩角差的正弦函數公式化簡后，利用正弦函數的值域即可得到距離的最小值.
試題解析：（1）
為圓心是
，半徑是1的圓， 
為中心是坐標原點，焦點在
軸，長半軸長是8，短半軸長是3的橢圓.
（2）當
時， 
，故
的普通方程為
， 
到
的距離
所以當
時， 
取得最小值
.
科目：高中數學 來源： 題型：
【題目】在如圖所示的空間四邊形ABCD中，E，F，G，H分別是AB，BC，CD，AD的中點，則圖中共有多少對線面平行關系？（ ）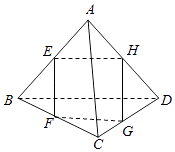 
A.2對
B.4對
C.6對
D.8對
查看答案和解析>>
科目：高中數學 來源： 題型：
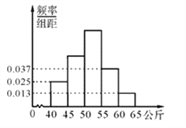
【題目】人的體重是人的身體素質的重要指標之一．某校抽取了高二的部分學生，測出他們的體重（公斤），體重在40公斤至65公斤之間，按體重進行如下分組：第1組[40,45)，第2組[45,50)，第3組[50,55)，第4組[55,60)，第5組[60,65]，并制成如圖所示的頻率分布直方圖，已知第1組與第3組的頻率之比為1:3，第3組的頻數為90．
（Ⅰ）求該校抽取的學生總數以及第2組的頻率；
（Ⅱ）學校為進一步了解學生的身體素質，在第1組、第2組、第3組中用分層抽樣的方法抽取6人進行測試．若從這6人中隨機選取2人去共同完成某項任務，求這2人來自于同一組的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市在對高三學生的4月理科數學調研測試的數據統計顯示，全市10000名學生的成績服從正態分布
，現從甲校100分以上（含100分）的200份試卷中用系統抽樣的方法抽取了20份試卷來分析，統計如下：
（注：表中試卷編號
）
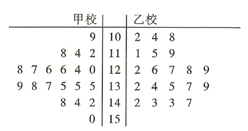
（1）列出表中試卷得分為126分的試卷編號（寫出具體數據）；
（2）該市又從乙校中也用系統抽樣的方法抽取了20份試卷，將甲乙兩校這40份試卷的得分制作了莖葉圖（如圖6），試通過莖葉圖比較兩校學生成績的平均分及分散程度（均不要求計算出具體值，給出結論即可）；
（3）在第（2）問的前提下，從甲乙兩校這40名學生中，從成績在140分以上（含140分）的學生中任意抽取3人，該3人在全市前15名的人數記為
，求
的分布列和期望.
（附：若隨機變量
服從正態分布
，則
， 
， 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若不等式a|x|＞x2﹣ 
對任意x∈[﹣1，1]都成立，則實數a的取值范圍是（ ）
A.（ ，1）∪（1，+∞）
B.（0， ）∪（1，+∞）??
C.（ ，1）∪（1，2）
D.（0， ）∪（1，2）
查看答案和解析>>
科目：高中數學 來源： 題型：
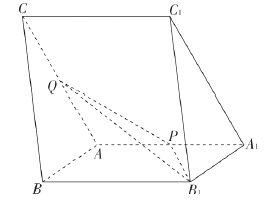
【題目】如圖，三棱柱
中， 
， 
， 
分別為棱
的中點.
（1）在平面
內過點
作
平面
交
于點
，并寫出作圖步驟，但不要求證明.
（2）若側面
側面
，求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】己知直線2x+y﹣8=0與直線x﹣2y+1=0交于點P．
（1）求過點P且平行于直線4x﹣3y﹣7=0的直線11的方程；（結果都寫成一般方程形式）
（2）求過點P的所有直線中使原點O到此直線的距離最大的直線12的方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
