
【題目】己知函數![]() .
.
(1)當![]() 時,求
時,求![]() 的極值;
的極值;
(2)當![]() 時,函數
時,函數![]() 的圖象與函數
的圖象與函數![]() 的圖象有唯一的交點,求
的圖象有唯一的交點,求![]() 的取值集合.
的取值集合.
【答案】(1)函數![]() 的極大值是
的極大值是![]() ,無極小值;(2)
,無極小值;(2)![]() .
.
【解析】
(1)當![]() 時,
時,![]() ,由導數為零,解得
,由導數為零,解得![]() ,從而可知
,從而可知![]() 隨
隨![]() 的變化,進而可求極值;
的變化,進而可求極值;
(2)設設![]() ,則
,則![]() 與
與![]() 只有一個交點,即
只有一個交點,即![]() 只有一個根,設
只有一個根,設![]() ,結合導數可知,當
,結合導數可知,當![]() 時,
時,![]() 有最大值為
有最大值為![]() ,畫出
,畫出![]() 草圖,可求出
草圖,可求出![]() 的取值集合.
的取值集合.
(1)解:當![]() 時,
時,![]() ,則
,則![]() ,解得
,解得![]() ,
,
則![]() 隨
隨![]() 的變化如表所示
的變化如表所示
|
|
|
|
|
| 0 |
|
|
|
|
|
所以函數![]() 的極大值是
的極大值是![]() ,無極小值;
,無極小值;
(2)解:設![]() ,則
,則![]() 與
與![]() 只有一個交點,其中
只有一個交點,其中![]() ,
,
則![]() 只有一個根,即
只有一個根,即![]() 只有一個根,
只有一個根,
設![]() ,則
,則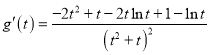 ,
,![]()
令![]() ,則
,則![]() ,設
,設![]() ,
,
則令![]() ,解得
,解得![]() ,則
,則![]() 隨
隨![]() 的變化如下表
的變化如下表
|
|
|
|
|
| 0 |
|
|
|
|
則當![]() 時,
時,![]() 取最小值為
取最小值為![]() ,
,
所以![]() ,即
,即![]() .
.
所以![]() 在
在![]() 上單調遞減,因此
上單調遞減,因此![]() 只有一個根,即
只有一個根,即![]() ,
,
當![]() 時,
時,![]() ,
,![]() 遞增;當
遞增;當![]() 時,
時,![]() ,
,![]() 遞減,
遞減,
所以,當![]() 時,
時,![]() 有最大值為
有最大值為![]() ,則
,則![]() 簡圖如圖所示,
簡圖如圖所示,
由題意知,![]() 與
與![]() 圖像只有一個交點,而
圖像只有一個交點,而![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以![]() 的取值集合為
的取值集合為![]() .
.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率
的離心率![]() ,且橢圓過點
,且橢圓過點![]()
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 在橢圓
在橢圓![]() 上,
上,![]() 是坐標原點,若
是坐標原點,若![]() ,判定四邊形
,判定四邊形![]() 的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
的面積是否為定值?若為定值,求出該定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某縣精準扶貧攻堅力公室決定派遣8名干部(5男3女)分成兩個小組,到該縣甲、乙兩個貧困村去參加扶貧工作,若要求每組至少3人,且每組均有男干部參加,則不同的派遣方案共有______種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“互倒函數”的定義如下:對于定義域內每一個![]() ,都有
,都有![]() 成立,若現在已知函數
成立,若現在已知函數![]() 是定義域在
是定義域在![]() 的“互倒函數”,且當
的“互倒函數”,且當![]() 時,
時,![]() 成立.若函數
成立.若函數![]() (
(![]() )都恰有兩個不同的零點,則實數
)都恰有兩個不同的零點,則實數![]() 的取值范圍是( )
的取值范圍是( )
A.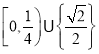 B.
B.![]() C.
C.![]() D.
D.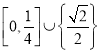
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖,從甲地到丙地要經過兩個十字路口(十字路口![]() 與十字路口
與十字路口![]() ),從乙地到丙地也要經過兩個十字路口(十字路口
),從乙地到丙地也要經過兩個十字路口(十字路口![]() 與十字路口
與十字路口![]() ),設各路口信號燈工作相互獨立,且在
),設各路口信號燈工作相互獨立,且在![]() ,
,![]() ,
,![]() ,
,![]() 路口遇到紅燈的概率分別為
路口遇到紅燈的概率分別為![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求一輛車從乙地到丙地至少遇到一個紅燈的概率;
(2)若小方駕駛一輛車從甲地出發,小張駕駛一輛車從乙地出發,他們相約在丙地見面,記![]() 表示這兩人見面之前車輛行駛路上遇到的紅燈的總個數,求
表示這兩人見面之前車輛行駛路上遇到的紅燈的總個數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右頂點分別為C、D,且過點
的左、右頂點分別為C、D,且過點![]() ,P是橢圓上異于C、D的任意一點,直線PC,PD的斜率之積為
,P是橢圓上異于C、D的任意一點,直線PC,PD的斜率之積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)O為坐標原點,設直線CP交定直線x = m于點M,當m為何值時,![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com