【題目】已知拋物線
上一點
到其焦點下的距離為10.
（1）求拋物線C的方程；
（2）設過焦點F的的直線
與拋物線C交于
兩點，且拋物線在兩點處的切線分別交x軸于
兩點，求
的取值范圍.
科目：高中數學 來源： 題型：
【題目】為培養學生的閱讀習慣，某校開展了為期一年的“弘揚傳統文化，閱讀經典名著”活動. 活動后，為了解閱讀情況，學校統計了甲、乙兩組各10名學生的閱讀量（單位：本），統計結果用莖葉圖記錄如下，乙組記錄中有一個數據模糊，無法確認，在圖中以a表示.
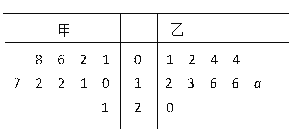
（Ⅰ）若甲組閱讀量的平均值大于乙組閱讀量的平均值，求圖中a的所有可能取值；
（Ⅱ）將甲、乙兩組中閱讀量超過15本的學生稱為“閱讀達人”. 設
，現從所有的“閱讀達人”里任取2人，求至少有1人來自甲組的概率；
（Ⅲ）記甲組閱讀量的方差為
. 若在甲組中增加一個閱讀量為10的學生，并記新得到的甲組閱讀量的方差為
，試比較，的大小.（結論不要求證明）
（注：
，其中
為數據
的平均數）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司租賃甲、乙兩種設備生產
、
兩類產品，甲種設備每天能生產類產品
件和類產品
件，乙種設備每天能生產類產品
件和類產品
件．已知設備甲每天的租賃費為
元，設備乙每天的租賃費為
元，現該公司至少要生產類產品
件，類產品
件，求所需租賃費最少為多少元？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某地隨著經濟的發展，居民收入逐年增長，下表是該地一建設銀行連續五年的儲蓄存款（年底余額），如下表1：
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y（千億元） | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便，工作人員將上表的數據進行了處理， 
得到下表2：
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（Ⅰ）求z關于t的線性回歸方程；
（Ⅱ）用所求回歸方程預測到2020年年底，該地儲蓄存款額可達多少？
（附：對于線性回歸方程
，其中
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，點D、E、F分別為線段A1C1、AB、A1A的中點，A1A＝AC＝BC，∠ACB＝90°．求證：
（1）DE∥平面BCC1B1；
（2）EF⊥平面B1CE．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
給出下列4個命題：①當且僅當
時，
是偶函數；②函數一定存在零點；③函數在區間
上單調遞減；④當
時，函數的最小值為
，那么所有真命題的序號是_______.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在數列
中，
.從數列中選出
項并按原順序組成的新數列記為
，并稱為數列的
項子列.例如數列
、
、
、
為的一個
項子列.
（1）試寫出數列的一個
項子列，并使其為等差數列；
（2）如果為數列的一個
項子列，且為等差數列，證明：的公差
滿足
；
（3）如果
為數列的一個
項子列，且為等比數列，證明：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓
：
（
）,左、右焦點分別是
、
且
,以為圓心,3為半徑的圓與以為圓心,1為半徑的圓相交于橢圓上的點
（1）求橢圓的方程；
（2）設橢圓
：
,
為橢圓上任意一點,過點的直線
交橢圓于
兩點,射線
交橢圓于點
①求
的值；
②令
,求
的面積
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設點
、
的坐標分別為
和
，動點P滿足
，設動點P的軌跡為
，以動點P到點距離的最大值為長軸，以點、為左、右焦點的橢圓為
，則曲線和曲線的交點到
軸的距離為_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
