【題目】以
表示值域為
的函數組成的集合，
表示具有如下性質的函數
組成的集合：對于函數，存在一個正數
，使得函數的值域包含于區間
。例如，當
，
時，
，
。則下列命題中正確的是：（ ）
A.設函數
的定義域為
，則“
”的充要條件是“
，
，
”
B.函數
的充要條件是有最大值和最小值
C.若函數，
的定義域相同，且，
，則
D.若函數
有最大值，則
【答案】ACD
【解析】
A選項中，根據函數的定義域、值域的定義，轉化成用簡易邏輯語言表示出來；
B選項中舉反例保證函數的值域為集合
的子集，但值域是一個開區間，從而說明函數沒有最值；C選項中從并集的角度認識函數值域，可以發現
，從而發現命題正確；D選項中從極限的角度證明
，
均不成立，所以
，再求出函數
的值域為
，從而得到命題D正確.
對A，“
”即函數值域為
，“
，
，
”表示的是函數可以在中任意取值，故有：設函數的定義域為
，則“”的充要條件是“，，”，
命題A是真命題；
對B，若函數
，即存在一個正數
，使得函數的值域包含于區間．
．例如：函數滿足
，則有
，此時，無最大值，無最小值．命題B“若函數，則有最大值和最小值．”是假命題；
對C，若函數，
的定義域相同，且，
，則值域為，
，并且存在一個正數，使得
，
，則
．命題C是真命題．
對D，
函數
有最大值，假設，當
時，
，
，
，則
，與題意不符； 假設，當
時，
，
，，則，與題意不符.
，即函數
，當
時，
，
，即
；當
時，
；當
時，
，
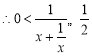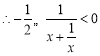，即
．
，即，故命題D是真命題．
故選：ACD.
科目：高中數學 來源： 題型：
【題目】已知奇函數f（x）=（a-x）|x|，常數a∈R，且關于x的不等式mx2+m＞f[f（x）]對所有的x∈[-2，2]恒成立，則實數m的取值范圍是______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動點P到定點
的距離比它到直線
的距離小2，設動點P的軌跡為曲線C．
求曲線C的方程；
若直線
與曲線C和圓
從左至右的交點依次為A，B，C，D求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
．
（1）當
時，函數
恒有意義，求實數
的取值范圍；
（2）是否存在這樣的實數，使得函數f（x）在區間
上為減函數，并且最大值為
？如果存在，試求出的值；如果不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，河的兩岸分別有生活小區
和
，其中
，
三點共線，
與
的延長線交于點
，測得
，
，
，
，
，若以
所在直線分別為
軸建立平面直角坐標系
則河岸
可看成是曲線
（其中
是常數）的一部分，河岸
可看成是直線
（其中
為常數）的一部分．
（1）求
的值．
（2）現準備建一座橋
，其中
分別在
上，且
，
的橫坐標為
．寫出橋的長
關于的函數關系式
，并標明定義域；當為何值時，取到最小值？最小值是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
與直線
相切，設點
為圓上一動點， 
軸于
，且動點
滿足
，設動點
的軌跡為曲線
．
（1）求曲線
的方程；
（2）直線
與直線
垂直且與曲線
交于
兩點，求
面積的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種蔬菜從1月1日起開始上市，通過市場調查，得到該蔬菜種植成本
（單位：元/
）與上市時間
（單位：10天）的數據如下表：
時間 | 5 | 11 | 25 |
種植成本 | 15 | 10.8 | 15 |
（1）根據上表數據，從下列函數：
，
，
，
中（其中
），選取一個合適的函數模型描述該蔬菜種植成本與上市時間的變化關系；
（2）利用你選取的函數模型，求該蔬菜種植成本最低時的上市時間及最低種植成本.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市每年春節前后,由于大量的煙花炮竹的燃放,空氣污染較為嚴重．該市環保研究所對近年春節前后每天的空氣污染情況調查研究后發現,每天空氣污染的指數．f（t），隨時刻t（時）變化的規律滿足表達式
，其中a為空氣治理調節參數,且a∈（0，1）．
(1)令
,求x的取值范圍；
(2)若規定每天中f（t）的最大值作為當天的空氣污染指數,要使該市每天的空氣污染指數不超過5,試求調節參數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
