Question

【題目】某公司在招聘員工時，要進行筆試，面試和實習三個過程．筆試設(shè)置了3個題，每一個題答對得5分，否則得0分．面試則要求應(yīng)聘者回答3個問題，每一個問題答對得5分，否則得0分．并且規(guī)定在筆試中至少得到10分，才有資格參加面試，而筆試和面試得分之和至少為25分，才有實習的機會．現(xiàn)有甲去該公司應(yīng)聘，假設(shè)甲答對筆試中的每一個題的概率為，答對面試中的每一個問題的概率為．

（1）求甲獲得實習機會的概率；

（2）設(shè)甲在去應(yīng)聘過程中的所得分數(shù)為隨機變量，求的分布列和數(shù)學期望．

Answer 1

【答案】（1）；（2）分布列見解析，

【解析】

（1）筆試和面試得分之和為25分的情況為：筆試和面試得分分別為10，15；或15，10．利用相互獨立與互斥事件概率計算公式即可得出．筆試和面試得分之和為30分的情況為：筆試和面試得分都為15．利用相互獨立與互斥事件概率計算公式即可得出．

（2）的取值為0，5，10，15，20，25，30，對筆試和面試得分情況分類討論，分別利用相互獨立與互斥事件概率計算公式即可得出．

（1）筆試和面試得分之和為25分的概率為．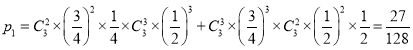

筆試和面試得分之和為30分的概率為．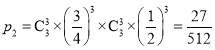

∴甲獲得實習機會的概率．

（2）的取值為0，5，10，15，20，25，30，

，，，

．

．

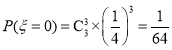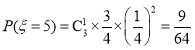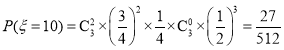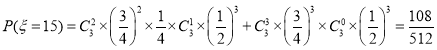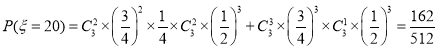由（1）可知：筆試和面試得分之和為25分的概率．

筆試和面試得分之和為30分的概率．

∴

．