
【題目】如圖,四棱錐![]() 中,
中,![]() ,
,![]() ,
,![]() 與
與![]() 都是等邊三角形,且點
都是等邊三角形,且點![]() 在底面
在底面![]() 上的射影為
上的射影為![]() .
.

(1)證明:![]() 為
為![]() 的中點;
的中點;
(2)求異面直線![]() 與
與![]() 所成角的大小.
所成角的大小.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)連接AC,取AC的中點N,連接MN,DN,利用線面垂直的判定證明點M在底面上的射影為N,結合點M在底而ABCD上的射影為O,可得N與O重合,即O為AC的中點;
(2)設![]() ,
,![]() ,求解三角形可得
,求解三角形可得![]() .再由DA=DC,O是AC的中點,得
.再由DA=DC,O是AC的中點,得![]() ,得到
,得到![]() ,故異面直線MD與BC所成角為
,故異面直線MD與BC所成角為![]() .在
.在![]() 中求解
中求解![]() ,可得異面直線
,可得異面直線![]() 與
與![]() 所成的角.
所成的角.
(1)證明:接![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() 、
、![]() ,
,
∵![]() 與
與![]() 都是等邊三角形且公共邊為
都是等邊三角形且公共邊為![]() ,
,
∴![]() ,
,
又∵![]() 是
是![]() 的中點,
的中點,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 平面
平面![]() ,故點
,故點![]() 在底面
在底面![]() 上的射影為
上的射影為![]() ,
,
又已知點![]() 在底面
在底面![]() 上的射影為
上的射影為![]() ,
,
∴![]() 與
與![]() 重合即
重合即![]() 為
為![]() 的中點;
的中點;

(2)設![]() ,
,![]() ,
,
∵![]() ,
,
![]() 為等腰直角三角形,
為等腰直角三角形,
則![]() ,
,![]() ,
,
![]() ,
,
![]()
則![]() ,
,
∴![]() ,
,
故![]() ,
,
又∵![]() ,
,![]() 是
是![]() 的中點,
的中點,
∴![]() ,
,
∴![]() ,
,
故異面直線![]() 與
與![]() 所成的角為
所成的角為![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
即異面直線![]() 與
與![]() 所成的角為
所成的角為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的長軸長為
的長軸長為![]() ,點
,點![]() 、
、![]() 、
、![]() 為橢圓上的三個點,
為橢圓上的三個點,![]() 為橢圓的右端點,
為橢圓的右端點,![]() 過中心
過中心![]() ,且
,且![]() ,
,![]() .
.

(1)求橢圓的標準方程;
(2)設![]() 、
、![]() 是橢圓上位于直線
是橢圓上位于直線![]() 同側的兩個動點(異于
同側的兩個動點(異于![]() 、
、![]() ),且滿足
),且滿足![]() ,試討論直線
,試討論直線![]() 與直線
與直線![]() 斜率之間的關系,并求證直線
斜率之間的關系,并求證直線![]() 的斜率為定值.
的斜率為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 是橢圓
是橢圓![]() 的左、右頂點,
的左、右頂點,![]() 為橢圓上異于
為橢圓上異于![]() 、
、![]() 的一點.
的一點.
(1)![]() 是橢圓
是橢圓![]() 的上頂點,且直線
的上頂點,且直線![]() 與直線
與直線![]() 垂直,求點
垂直,求點![]() 到
到![]() 軸的距離;
軸的距離;
(2)過點![]() 的直線
的直線![]() (不過坐標原點)與橢圓
(不過坐標原點)與橢圓![]() 交于
交于![]() 、
、![]() 兩點,且點
兩點,且點![]() 在
在![]() 軸上方,點
軸上方,點![]() 在
在![]() 軸下方,若
軸下方,若![]() ,求直線
,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代數學名著《九章算術》中有這樣一個問題:今有牛、馬、羊食人苗,苗主責之粟五斗,羊主曰:“我羊食半馬.”馬主曰:“我馬食半牛.”今欲衰償之,問各出幾何?此問題的譯文是:今有牛、馬、羊吃了別人的禾苗,禾苗主人要求賠償5斗粟.羊主人說:“我羊所吃的禾苗只有馬的一半.”馬主人說:“我馬所吃的禾苗只有牛的一半.”打算按此比例償還,他門各應償還多少?該問題中,1斗為10升,則羊主人應償還多少升粟?( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點O,左右焦點分別為![]() ,
,![]() 的橢圓的離心率為
的橢圓的離心率為![]() ,焦距為
,焦距為![]() ,A,B是橢圓上兩點.
,A,B是橢圓上兩點.
(1)若直線![]() 與以原點為圓心的圓相切,且
與以原點為圓心的圓相切,且![]() ,求此圓的方程;
,求此圓的方程;
(2)動點P滿足:![]() ,直線
,直線![]() 與
與![]() 的斜率的乘積為
的斜率的乘積為![]() ,求動點P的軌跡方程.
,求動點P的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐S﹣ABCD中,側面SCD為鈍角三角形且垂直于底面ABCD,![]() ,點M是SA的中點,
,點M是SA的中點,![]() ,
,![]() ,
,![]() .
.
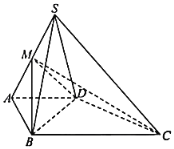
(1)求證:![]() 平面SCD;
平面SCD;
(2)若直線SD與底面ABCD所成的角為![]() ,求平面MBD與平面SBC所成的銳二面角的余弦值.
,求平面MBD與平面SBC所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某教研機構隨機抽取某校20個班級,調查各班關注漢字聽寫大賽的學生人數,根據所得數據的莖葉圖,以組距為5將數據分組成![]() 時,所作的頻率分布直方圖如圖所示,則原始莖葉圖可能是( )
時,所作的頻率分布直方圖如圖所示,則原始莖葉圖可能是( )
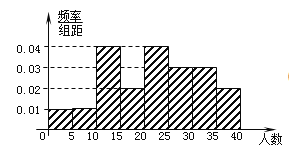
A.  B.
B. 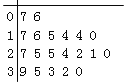
C. 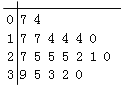 D.
D. 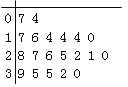
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com