【題目】設p:實數x滿足
,其中a≠0,q:實數x滿足
.
(I)若a=1,且p∧q為真,求實數x的取值范圍.
(II)若p是q的必要不充分條件,求實數a的取值范圍.
【答案】(1)(2,3),(2) a∈(1,2]
【解析】試題分析：（1）化簡條件p,q，根據p∧q為真,可求出；
（2）化簡命題，寫成集合，由題意轉化為(2,3]
(3a,a)即可求解.
試題解析：
(I)由
,得q:2<x≤3.
當a=1時,由x2-4x+3<0,得p:1<x<3,
因為p∧q為真,所以p真,q真.
由
得
所以實數x的取值范圍是(2,3).
(II)由x2-4ax+3a2<0,得(x-a)(x-3a)<0.
①當a>0時,p:a<x<3a,
由題意,得(2,3](a,3a),所以即1<a≤2;
②當a<0時,p:3a<x<a,
由題意,得(2,3](3a,a),所以無解.
綜上,可得a∈(1,2].
新題型全程檢測期末沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】某大理石工廠初期花費98萬元購買磨大理石刀具，第一年需要各種費用12萬元，從第二年起，每年所需費用比上一年增加4萬元，該大理石加工廠每年總收入50萬元.
（1）到第幾年末總利潤最大，最大值是多少？
（2）到第幾年末年平均利潤最大，最大值是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列有關結論正確的個數為（ ）
①小趙、小錢、小孫、小李到4個景點旅游，每人只去一個景點，設事件
=“4個人去的景點不相同”，事件
“小趙獨自去一個景點”，則
；
②設函數
存在導數且滿足
，則曲線
在點
處的切線斜率為-1；
③設隨機變量
服從正態分布
，若
，則
與
的值分別為
；
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市政府為了節約生活用電，計劃在本市試行居民生活用電定額管理，即確定一個居民月用電量標準
，用電量不超過
的部分按平價收費，超出
的部分按議價收費．為此，政府調查了100戶居民的月平均用電量（單位：度），以
， 
， 
， 
， 
， 
， 
分組的頻率分布直方圖如圖所示．
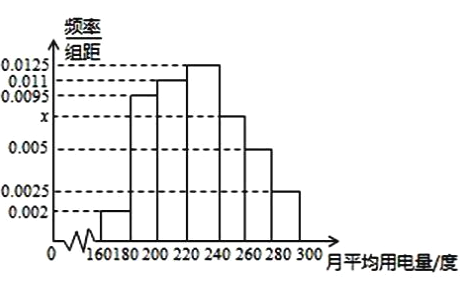
（1）求直方圖中
的值；
（2）求月平均用電量的眾數和中位數；
（3）如果當地政府希望使
左右的居民每月的用電量不超出標準，根據樣本估計總體的思想，你認為月用電量標準
應該定為多少合理？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某廠擬生產甲、乙兩種適銷產品，每件銷售收入分別為3萬元、2萬元，甲、乙產品都需要在
兩種設備上加工，在每臺
上加工1件甲所需工時分別是1
、2
，加工1件乙所需工時分別為2
、1
， 
兩種設備每月有效使用臺時數分別為400
和500
，如何安排生產可使收入最大？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
，（a＞0）．
（1）當a=2時，證明函數f（x）不是奇函數；
（2）判斷函數f（x）的單調性，并利用函數單調性的定義給出證明；
（3）若f（x）是奇函數，且f（x）﹣x2+4x≥m在x∈[﹣2，2]時恒成立，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于定義域為D的函數y=f（x），如果存在區間[m，n]D，同時滿足：
①f（x）在[m，n]內是單調函數；
②當定義域是[m，n]時，f（x）的值域也是[m，n]．
則稱[m，n]是該函數的“和諧區間”．
（1）證明：[0，1]是函數y=f（x）=x2的一個“和諧區間”．
（2）求證：函數 
不存在“和諧區間”．
（3）已知：函數 
（a∈R，a≠0）有“和諧區間”[m，n]，當a變化時，求出n﹣m的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
在x=1處的切線與直線
平行。
（Ⅰ）求a的值并討論函數y=f(x)在
上的單調性。
（Ⅱ）若函數
(
為常數)有兩個零點
，
(1)求m的取值范圍；
(2)求證： 
。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
