
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為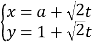 (
(![]() 為參數,
為參數, ![]() ),以
),以![]() 為極點,
為極點, ![]() 軸非負半軸為極軸,建立極坐標系,曲線
軸非負半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】已知一家公司生產某種品牌服裝的年固定成本為![]() 萬元,每生產
萬元,每生產![]() 千件需另投入
千件需另投入![]() 萬元.設該公司一年內共生產該品牌服裝
萬元.設該公司一年內共生產該品牌服裝![]() 千件并全部銷售完,每千件的銷售收入為
千件并全部銷售完,每千件的銷售收入為![]() 萬元,且
萬元,且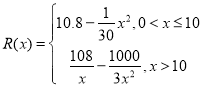 .
.
(1)寫出年利潤![]() (萬元)關于年產量
(萬元)關于年產量![]() (千件)的函數解析式;
(千件)的函數解析式;
(2)年產量為多少千件時,該公司在這一品牌服裝的生產中所獲得利潤最大?(注:年利潤=年銷售收入-年總成本)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 的直角頂點
的直角頂點![]() 在
在![]() 軸上,點
軸上,點![]() 為斜邊
為斜邊![]() 的中點,且
的中點,且![]() 平行于
平行于![]() 軸.
軸.
(Ⅰ)求點![]() 的軌跡方程;
的軌跡方程;
(Ⅱ)設點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() 與
與![]() 的另一個交點為
的另一個交點為![]() .以
.以![]() 為直徑的圓交
為直徑的圓交![]() 軸于
軸于![]() 即此圓的圓心為
即此圓的圓心為![]() ,
,![]() 求
求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠有4臺大型機器,在一個月中,一臺機器至多出現1次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需1名工人進行維修,每臺機器出現故障需要維修的概率為![]() .
.
(1)若出現故障的機器臺數為![]() ,求
,求![]() 的分布列;
的分布列;
(2) 該廠至少有多少名工人才能保證每臺機器在任何時刻同時出現故障時能及時進行維修的概率不少于90%?
(3)已知一名工人每月只有維修1臺機器的能力,每月需支付給每位工人1萬元的工資,每臺機器不出現故障或出現故障能及時維修,就使該廠產生5萬元的利潤,否則將不產生利潤,若該廠現有2名工人,求該廠每月獲利的均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某部影片的盈利額(即影片的票房收入與固定成本之差)記為y,觀影人數記為x,其函數圖象如圖(1)所示.由于目前該片盈利未達到預期,相關人員提出了兩種調整方案,圖(2)、圖(3)中的實線分別為調整后y與x的函數圖象,給出下列四種說法,①圖(2)對應的方案是:提高票價,并提高成本;②圖(2)對應的方案是:保持票價不變,并降低成本;③圖(3)對應的方案是:提高票價,并保持成本不變;④圖(3)對應的方案是:提高票價,并降低成本.其中,正確的說法是( )

A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中石化集團獲得了某地深海油田區塊的開采權,集團在該地區隨機初步勘探了部分兒口井,取得了地質資料.進入全面勘探時期后,集團按網絡點來布置井位進行全面勘探. 由于勘探一口井的費用很高,如果新設計的井位與原有井位重合或接近,便利用舊井的地質資料,不必打這口新井,以節約勘探費用.勘探初期數據資料見如表:

(Ⅰ)1~6號舊井位置線性分布,借助前5組數據求得回歸直線方程為![]() ,求
,求![]() ,并估計
,并估計![]() 的預報值;
的預報值;
(Ⅱ)現準備勘探新井![]() ,若通過1、3、5、7號井計算出的
,若通過1、3、5、7號井計算出的![]() 的值(
的值(![]() 精確到0.01)相比于(Ⅰ)中
精確到0.01)相比于(Ⅰ)中![]() 的值之差不超過10%,則使用位置最接近的已有舊井
的值之差不超過10%,則使用位置最接近的已有舊井![]() ,否則在新位置打開,請判斷可否使用舊井?
,否則在新位置打開,請判斷可否使用舊井?
(參考公式和計算結果: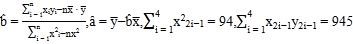 )
)
(Ⅲ)設出油量與勘探深度的比值![]() 不低于20的勘探并稱為優質井,那么在原有井號1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是優質井的概率.
不低于20的勘探并稱為優質井,那么在原有井號1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是優質井的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
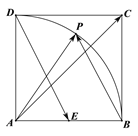
【題目】如圖,在邊長為1的正方形ABCD中,E為AB的中點,P為以A為圓心,AB為半徑的圓弧(在正方形內,包括邊界點)上的任意一點,則![]() 的取值范圍是________; 若向量
的取值范圍是________; 若向量![]() ,則
,則![]() 的最小值為_________.
的最小值為_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,
, ![]() 為焦點是
為焦點是![]() 的拋物線上一點,
的拋物線上一點, ![]() 為直線
為直線![]() 上任一點,
上任一點, ![]() 分別為橢圓
分別為橢圓![]() 的上,下頂點,且
的上,下頂點,且![]() 三點的連線可以構成三角形.
三點的連線可以構成三角形.
(1)求橢圓![]() 的方程;
的方程;
(2)直線![]() 與橢圓
與橢圓![]() 的另一交點分別交于點
的另一交點分別交于點![]() ,求證:直線
,求證:直線![]() 過定點.
過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com