Question

【題目】(2015·江蘇）已知集合X={1，2，3}，Yn={1,2,3...,n}(nN*)，Sn={(a,b)|a整除b或b整除a， aX, bYn}, 令f(n)表示集合Sn所包含元素的個數。
（1）寫出f（6）的值；
（2）當n≥6時，寫出f(n)的表達式，并用數學歸納法證明.

Answer 1

【答案】
（1）

13

（2）

f(n)=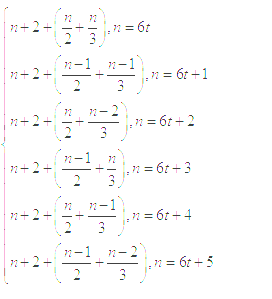

【解析】
(1) 根據題意按a分類計數，a=1, b=1,2,3,4,5,6, a=2, b=1,2,4,5, a=3,b=1,3,6 共13個（2）由（1）知a=1, b=1,2,3,...,n, a=2, b=1,2,4,....,2k, a=3,b=1,3,...,3k(kN*), ，所以當n≥6時，f(n)的表達方式要按2x3=6除的余數進行分類，最后不難利用數學歸納法進行證明。
（1）f(6)=13, (2)當n≥6時， f(n)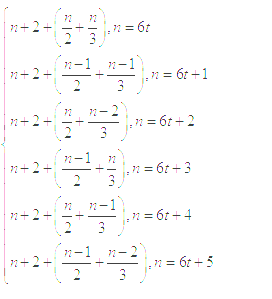(tN*).
下面用數學歸納法證明:①n=6時，f（6）=6+2+=13, 結論成立。
②假設n=k(k≥6)時結論成立，那么n=k+1時，Sk+1在Sk的基礎上新增的元素在（1，k+1), (2, k+1), (3, k+1)中產生，分以下情形討論。
1）若k+1=6t, 則k=6(t-1)+5, 此時有f(k+1)=f(k)+3=k+2+++3=(k+1)+2++, 結論成立。
2）若k+1=6t+1, 則k=6t, 此時有f(k+1)=f(k)+1=k+2+++1=(k+1)+2++, 結論成立。
3)若k+1=6t+1, 則k=6t+1, 此時有f(k+1)=f(k)+2=k+2+++2=(k+1)+2++, 結論成立。
4)若k+1=6t+3, 則k=6t+2, 此時有f(k+1)=f(k)+2=k+2+++2=(k+1)+2++, 結論成立。
5)若k+1=6t+4, 則k=6t+3, 此時有f(k+1)=f(k)+2=k+2+++2=(k+1)+2++, 結論成立。
5)若k+1=6t+5, 則k=6t+5, 此時有f(k+1)=f(k)+2=k+2+++1=(k+1)+2++, 結論成立。
綜上所述， 結論對滿足n≥6的自然數n 均成立。
【考點精析】認真審題，首先需要了解數學歸納法的定義(數學歸納法是證明關于正整數n的命題的一種方法)．