
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,直線
,直線![]() :
:![]() 交橢圓于
交橢圓于![]() ,
,![]() 兩點,
兩點,![]() ,且點
,且點![]() 在橢圓
在橢圓![]() 上,當
上,當![]() 時,
時,![]() .
.
(1)求橢圓方程;
(2)試探究四邊形![]() 的面積是否為定值,若是,求出此定值;若不是,請說明理由.
的面積是否為定值,若是,求出此定值;若不是,請說明理由.
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心坐標為
的圓心坐標為![]() ,且該圓經過點
,且該圓經過點![]() .
.
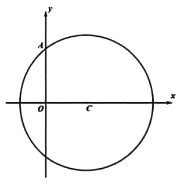
(1)求圓![]() 的標準方程;
的標準方程;
(2)若點![]() 也在圓
也在圓![]() 上,且弦
上,且弦![]() 長為8,求直線
長為8,求直線![]() 的方程;
的方程;
(3)直線![]() 交圓
交圓![]() 于
于![]() ,
,![]() 兩點,若直線
兩點,若直線![]() ,
,![]() 的斜率之積為2,求證:直線
的斜率之積為2,求證:直線![]() 過一個定點,并求出該定點坐標.
過一個定點,并求出該定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于曲線![]() ,有如下結論:
,有如下結論:
①曲線C關于原點對稱;
②曲線C關于直線x±y=0對稱;
③曲線C是封閉圖形,且封閉圖形的面積大于2π;
④曲線C不是封閉圖形,且它與圓x2+y2=2無公共點;
⑤曲線C與曲線![]() 有4個交點,這4點構成正方形.其中所有正確結論的序號為__.
有4個交點,這4點構成正方形.其中所有正確結論的序號為__.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P-ABCD中,底面ABCD為矩形,PD⊥平面ABCD,點E、F分別是AB和PC的中點.
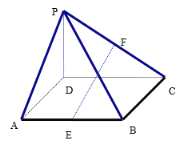
(1)求證:AB⊥平面PAD;
(2)求證:EF//平面PAD.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 上一點
上一點![]() 到左右兩個焦點
到左右兩個焦點![]() 的距離之和是4.
的距離之和是4.
(1)求橢圓的方程;
(2)已知過![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() 兩點,且兩點與左右頂點不重合,若
兩點,且兩點與左右頂點不重合,若![]() ,求四邊形
,求四邊形![]() 面積的最大值。
面積的最大值。
查看答案和解析>>
科目:高中數學 來源: 題型:
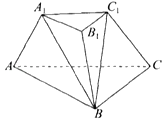
【題目】如圖,在三棱臺ABC﹣A1B1C1中,底面ABC是邊長為2的等邊三角形,上、下底面的面積之比為1:4,側面A1ABB1⊥底面ABC,并且A1A=A1B1,∠AA1B=90°.
(1)平面A1C1B∩平面ABC=l,證明:A1C1∥l;
(2)求平面A1C1B與平面ABC所成二面角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,在五邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是以
是以![]() 為斜邊的等腰直角三角形.現將
為斜邊的等腰直角三角形.現將![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,如圖②,記線段
,如圖②,記線段![]() 的中點為
的中點為![]() .
.
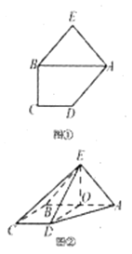
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 與平面
與平面![]() 所成的銳二面角的大小.
所成的銳二面角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著智能手機的普及,使用手機上網成為了人們日常生活的一部分,很多消費者對手機流量的需求越來越大.某通信公司為了更好地滿足消費者對流量的需求,準備推出一款流量包.該通信公司選了人口規模相當的![]() 個城市采用不同的定價方案作為試點,經過一個月的統計,發現該流量包的定價:
個城市采用不同的定價方案作為試點,經過一個月的統計,發現該流量包的定價: ![]() (單位:元/月)和購買總人數
(單位:元/月)和購買總人數![]() (單位:萬人)的關系如表:
(單位:萬人)的關系如表:
定價x(元/月) | 20 | 30 | 50 | 60 |
年輕人(40歲以下) | 10 | 15 | 7 | 8 |
中老年人(40歲以及40歲以上) | 20 | 15 | 3 | 2 |
購買總人數y(萬人) | 30 | 30 | 10 | 10 |
(Ⅰ)根據表中的數據,請用線性回歸模型擬合![]() 與
與![]() 的關系,求出
的關系,求出![]() 關于
關于![]() 的回歸方程;并估計
的回歸方程;并估計![]() 元/月的流量包將有多少人購買?
元/月的流量包將有多少人購買?
(Ⅱ)若把![]() 元/月以下(不包括
元/月以下(不包括![]() 元)的流量包稱為低價流量包,
元)的流量包稱為低價流量包,![]() 元以上(包括
元以上(包括![]() 元)的流量包稱為高價流量包,試運用獨立性檢驗知識,填寫下面列聯表,并通過計算說明是否能在犯錯誤的概率不超過
元)的流量包稱為高價流量包,試運用獨立性檢驗知識,填寫下面列聯表,并通過計算說明是否能在犯錯誤的概率不超過![]() 的前提下,認為購買人的年齡大小與流量包價格高低有關?
的前提下,認為購買人的年齡大小與流量包價格高低有關?
定價x(元/月) | 小于50元 | 大于或等于50元 | 總計 |
年輕人(40歲以下) | |||
中老年人(40歲以及40歲以上) | |||
總計 |
參考公式:其中![]()
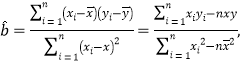
![]()
![]() 其中
其中![]()
參考數據:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com