
【題目】已知函數f(x)=ex-ax-1,其中e是自然對數的底數,實數a是常數.
(1)設a=e,求函數f(x)的圖象在點(1,f(1))處的切線方程;
(2)討論函數f(x)的單調性.
【答案】(1)![]() ; (2)答案見解析.
; (2)答案見解析.
【解析】
(1)求函數f(x)的導數,可寫出對應切線方程
(2) 對函數f(x)的導數值的正負分類,討論單調性。
(1)∵a=e,∴f(x)=ex-ex-1,
∴f′(x)=ex-e,f(1)=-1,f′(1)=0.
∴當a=e時,函數f(x)的圖象在點(1,f(1))處的切線方程為y=-1.
(2)∵f(x)=ex-ax-1,∴f′(x)=ex-a.
當a≤0時,f′(x)>0,故f(x)在![]() 上單調遞增;
上單調遞增;
當a>0時,由f′(x)=ex-a=0,得x=ln a,
∴當x<ln a時,f′(x)<![]() =0,當x>ln a時,f′(x)>
=0,當x>ln a時,f′(x)>![]() =0,
=0,
∴f(x)在(![]() ,ln a)上單調遞減,在(ln a,+∞)上單調遞增.
,ln a)上單調遞減,在(ln a,+∞)上單調遞增.
綜上,當a≤0時,f(x)在![]() 上單調遞增;
上單調遞增;
當a>0時,∴f(x)在(![]() ,ln a)上單調遞減,在(ln a,+∞)上單調遞增.
,ln a)上單調遞減,在(ln a,+∞)上單調遞增.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
【題目】已知直三棱柱![]() 中的底面為等腰直角三角形,
中的底面為等腰直角三角形,![]() ,點
,點![]() 分別是邊
分別是邊![]() ,
,![]() 上動點,若直線
上動點,若直線![]() 平面
平面![]() ,點
,點![]() 為線段
為線段![]() 的中點,則
的中點,則![]() 點的軌跡為
點的軌跡為![]()
![]()
A. 雙曲線的一支![]() 一部分
一部分![]() B. 圓弧
B. 圓弧![]() 一部分
一部分![]()
C. 線段![]() 去掉一個端點
去掉一個端點![]() D. 拋物線的一部分
D. 拋物線的一部分
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某花圃為提高某品種花苗質量,開展技術創新活動,在A,B實驗地分別用甲、乙方法培育該品種花苗.為觀測其生長情況,分別在實驗地隨機抽取各50株,對每株進行綜合評分,將每株所得的綜合評分制成如圖所示的頻率分布直方圖.記綜合評分為80及以上的花苗為優質花苗.
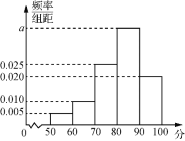
(1)求圖中a的值;
(2)用樣本估計總體,以頻率作為概率,若在A,B兩塊試驗地隨機抽取3棵花苗,求所抽取的花苗中的優質花苗數的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩名射手互不影響地進行射擊訓練,根據以往的數據統計,他們射擊成績的分布列如下表所示.
射手甲 | 射手乙 | ||||||
環數 |
|
|
| 環數 |
|
|
|
概率 |
|
|
| 概率 |
|
|
|
(1)若甲射手共有![]() 發子彈,一旦命中
發子彈,一旦命中![]() 環就停止射擊,求他剩余
環就停止射擊,求他剩余![]() 發子彈的概率;
發子彈的概率;
(2)若甲、乙兩名射手各射擊![]() 次,求
次,求![]() 次射擊中恰有
次射擊中恰有![]() 次命中
次命中![]() 環的概率;
環的概率;
(3)若甲、乙兩名射手各射擊![]() 次,記所得的環數之和為
次,記所得的環數之和為![]() ,求
,求![]() 的概率分布.
的概率分布.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)在![]() 中,內角A,B,C的對邊分別為a,b,c,R表示
中,內角A,B,C的對邊分別為a,b,c,R表示![]() 的外接圓半徑.
的外接圓半徑.
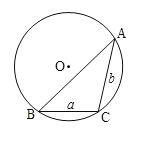
①如圖,在以O圓心、半徑為2的圓O中,![]() 和
和![]() 是圓O的弦,其中
是圓O的弦,其中![]() ,
,![]() ,求弦
,求弦![]() 的長;
的長;
②在![]() 中,若
中,若![]() 是鈍角,求證:
是鈍角,求證:![]() ;
;
(2)給定三個正實數a、b、R,其中![]() ,問:a、b、R滿足怎樣的關系時,以a、b為邊長,R為外接圓半徑的
,問:a、b、R滿足怎樣的關系時,以a、b為邊長,R為外接圓半徑的![]() 不存在、存在一個或存在兩個(全等的三角形算作同一個)?在
不存在、存在一個或存在兩個(全等的三角形算作同一個)?在![]() 存在的情況下,用a、b、R表示c.
存在的情況下,用a、b、R表示c.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系![]() ,以
,以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 過點P(-1,2),且傾斜角為
過點P(-1,2),且傾斜角為![]() ,圓
,圓![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求圓![]() 的普通方程和直線
的普通方程和直線![]() 的參數方程;
的參數方程;
(Ⅱ)設直線![]() 與圓
與圓![]() 交于M、N兩點,求
交于M、N兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com